Question 1073403: Circle T intersects the hyperbola y=1/x at (1,1), (3, 1/3), and two other points. What is the product of the y coordinates of the other two points? Please write in proof format. Thank you.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Circle T intersects the hyperbola y=1/x at (1,1), (3, 1/3), and two other points.
What is the product of the y coordinates of the other two points? Please write in proof format. Thank you.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The equation of the circle is
 = =  ,
for some "a", "b" and "r".
The equation of the hyperbola is y = ,
for some "a", "b" and "r".
The equation of the hyperbola is y =  (given !)
You will get the equation for common points (intersection points) if you substitute equation (2) into the equation (1).
You will get (given !)
You will get the equation for common points (intersection points) if you substitute equation (2) into the equation (1).
You will get
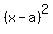 + + 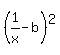 = =  , or , or
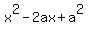 + + 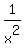 - - 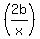 + + 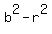 = 0.
Next multiply both sides by = 0.
Next multiply both sides by  to rid of denominators. You will get to rid of denominators. You will get
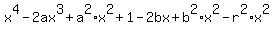 = 0, or, ordering by descending degrees of x = 0, or, ordering by descending degrees of x
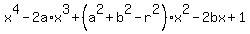 = 0.
The last equation is the 4-th degree equation. Its roots are x-coordinates of the common (intersection) points.
Two of the roots are given: they are x-coordinates of the given intersection points x= 1 and x= 3.
Two other roots are not known.
But, according to the Vieta's theorem for the equation of the degree 4, the product of four roots is the constant term
( ! - it is the KEY idea ! ).
Thus, = 0.
The last equation is the 4-th degree equation. Its roots are x-coordinates of the common (intersection) points.
Two of the roots are given: they are x-coordinates of the given intersection points x= 1 and x= 3.
Two other roots are not known.
But, according to the Vieta's theorem for the equation of the degree 4, the product of four roots is the constant term
( ! - it is the KEY idea ! ).
Thus, 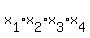 = = 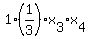 = 1, (1)
which implies = 1, (1)
which implies
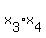 = = 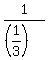 = 3. (2)
The problem asks about = 3. (2)
The problem asks about 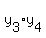 , but it is simply , but it is simply
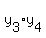 = = 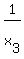 . .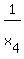 = = 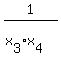 = =  due to (2).
So, the problem is solved and the answer is: the product of y-coordinates of the two other intersection points is
due to (2).
So, the problem is solved and the answer is: the product of y-coordinates of the two other intersection points is  .
Answer. The product of y-coordinates of the two other intersection points is .
Answer. The product of y-coordinates of the two other intersection points is  . .
Solved.
For Vieta's Theorem see this Wikipedia article.
|
|
|