Question 1069371: The radius of two concentric circles are 13cm and 8cm . AB is a diamerer of the bigger circle and BD is tangent to the smaller circle touching it at D. And intersecting the larger circle at P on producing. Find the length of AP
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
Answer. The length of AP is 13: |AP| = 13 cm.
Proof.
Consider two triangles, ODB and ABP, where O is the common center of the circles.
The triangle OBD is a right-angled triangle with the right angle at the vertex D, since the radius drawn to the tangent point
is perpendicular to the tangent line.
The triangle ABP is also a right-angled triangle with the right angle at the vertex P, since the angle APB lean on the diameter of the circle.
These two triangles are similar since they have the common acute angle ABP (same as OBD).
The similarity coefficient is 2:  =  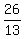= 2: it is the ratio of hypotenuses of the triangles.
Therefore, |AP| = 2.|OD| = 2*8 = 16 cm.
Answer. |AP| = 16 cm.
For properties of circles, their radii and tangent lines, that relevant to this problem, see the lessons
- A tangent line to a circle is perpendicular to the radius drawn to the tangent point
- An inscribed angle in a circle
in this site.
Also, you have this free of charge online textbook on Geometry
GEOMETRY - YOUR ONLINE TEXTBOOK
in this site.
The referred lessons are the part if this textbook under the topic
"Properties of circles, inscribed angles, chords, secants and tangents".
|
|
|
