SOLUTION: find the center and radius of the circle having equation x^2+y^2+2x-4y+1=0

We need to get it in the form  so we'll
know it has center (h,k) and radius r.

First we add -1 to both sides to get the constant off the left side:



Next we swap the 2nd and 3rd terms to get terms with the same letter
next to each other:




Put the addition of one blank after the +2x and another after the 
-4y since we are going to add something to both sides:



Next we calculate what goes in the first blank:

1. Multiply the coefficient of x, which is 2, by }, getting 
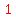2. Square that value:  , so  is what goes
in the first blank, and we also add it to the right side:

  

Next we calculate what goes in the second blank:

1. Multiply the coefficient of y, which is -4, by }, getting 
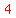2. Square that value:  , so  is 
what goes in the second blank, and we also add it to the right 
side:



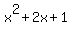The first three terms on the left  factors as  
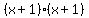or 

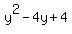The last three terms on the left  factors as  
or 

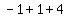The right side  becomes 

So we now have:



And we compare that to 
 

and we see that since , , and
since , . Also  so }

So the center is (h,k) = (-1,2) and the radius = r = 2.

Edwin