For what value/s of k will the system of equations x^2 + y^2 = 4 and y=kx+4 have exactly two points?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 = 4, (1)
y = kx + 4. (2)
Substitute the expression y = kx + 4 from (2) into equation (1). You will get
= 4, (1)
y = kx + 4. (2)
Substitute the expression y = kx + 4 from (2) into equation (1). You will get
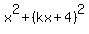 = 4.
Simplify
= 4.
Simplify
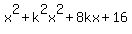 = 4,
= 4,
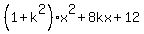 = 0.
In order for the last equation has two different real roots, the discriminant must be positive:
d = b^2 - 4ac = (8k)^2 - 4*(1+k^2)*12 > 0, or
64k^2 - 48k^2 - 48 > 0, or
16k^2 > 48, or
k^2 > 3, or
k <
= 0.
In order for the last equation has two different real roots, the discriminant must be positive:
d = b^2 - 4ac = (8k)^2 - 4*(1+k^2)*12 > 0, or
64k^2 - 48k^2 - 48 > 0, or
16k^2 > 48, or
k^2 > 3, or
k <  OR k >
OR k >  .
Answer. The solution set is (
.
Answer. The solution set is ( ,
, ) U (
) U ( ,
, ).
).