SOLUTION: Find the equation of the circle (in general form) tangent to the line 4x + 5y = 7 and concentric with the circle. (x-4)^2 +y^2 -5=0

The center of the circle (of both circles) is at the point (4,0).


Find the distance from the point (4,0) to the straight line 4x + 5y = 7.
For it, use the formula for the distance from the point to the straight line in a coordinate plane

(for example, from the lesson The distance from a point to a straight line in a coordinate plane in this site).

d =  = .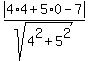

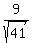    (Do not miss "d" with the diameter! In opposite, the "d" is the radius:

        r = 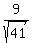,  and   = . )

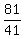Now the equation of the circle is 

     = .

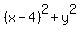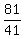Figure