We need to get it in the standard form, which is
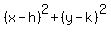
where (h,k) is the center and r is the radius.
---------------------------------------------
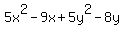
Divide through by the common coefficient of x² and y²
which is 5:
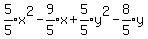
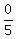Simplify:
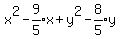
Put parentheses around the two terms in x and around the
two terms in y
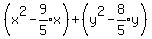
To complete the squares, we need to add a number to the
end of each parentheses, and to the right side:
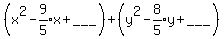
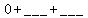so we put a blank where we need to add numbers.
To complete the square in the first parentheses:
1. Multiply the coefficient of x by 
:
2. Square that result:
3. Put that where the first blanks are on the left and right sides:
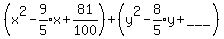
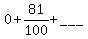To complete the square in the second parentheses, follow
the same procedure:
1. Multiply the coefficient of y by :
2. Square that result:
[Don't bother to reduce fractions yet]
3. Put that where the remaining blanks are on the left and right sides:
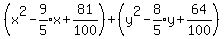
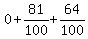The two parentheses factor into squares of binomials,
using the square roots of the numbers added (which are
actually the results of the two step 1's). Combine the
numbers on the right side 
[Again don't bother to reduce fractions yet]
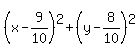
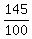
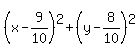
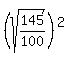
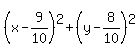
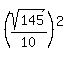Now you can reduce the 8/10 to 4/5:
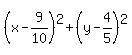
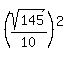Compare to:
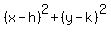
where (h,k) is the center and r is the radius.
And so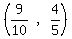 
is the center
and 
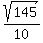is the radius.
Edwin
