Question 1042410: Use this photo: https://byuis.brainhoney.com/Resource/46824921,0/Assets/Media/Images/GEOM043_SB-5-4.jpg
a) Calculate the circumference of circle Q.
b) Approximate the area of the circle segment bounded by line DE and arc DE. (Hint: Use trigonometry as needed.)
c) Calculate the length of arc DE.
d) Calculate the area of circle Q.
e) Calculate the area of the sector bounded by line DQ, line EQ, and arc DE.
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website! Radius shown as 15 units. Area of the sector is  .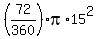
The angle each at D and E is some x measure according to  .
 .
NOW you can use Law Of Sines to find length of segment DE.
and you can use this to find the area of the triangle, which will let you answer question part (e).
Area of Triangle DQE
Isosceles, angles 54, 54, 72, one of the equal sides, 15 units.
--
Draw altitude from midpoint of DE to center point of circle, Q. Call this altitude, h. Call the midpoint on DE, the point H.
You have either of two right triangles, hypotenuse 15, leg QH, leg EH, angle at Q being  .
-
 .
What about lengths HD or HE?
Call this length, both being congruent, v.
 because first two are the legs and 15 is a hypotenuse.
-
 OR  .
Continuing for the area of the whole triangle,
 , because the entire BASE is 2v; and altitude is h.
The area between the arc and the triangle DQE is then:
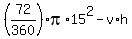 -----Simplify, substitute for v and h, simplify more, and finish.
|
|
|
