SOLUTION: In a Reflection,the image of the line y-2x=3 is the line 2y-x=9.Then What Is The Line Of Reflection?

Algebra ->  Points-lines-and-rays -> SOLUTION: In a Reflection,the image of the line y-2x=3 is the line 2y-x=9.Then What Is The Line Of Reflection?      Log On


   

Question 1038606: In a Reflection,the image of the line y-2x=3 is the line 2y-x=9.Then What Is The Line Of Reflection?
Found 2 solutions by solver91311, KMST:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


It is the line with a slope of 1 that passes through the intersection of the two given lines.

John

My calculator said it, I believe it, that settles it

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
ONE WAY TO THE ANSWER:
The slope of red%28y-2x=3%29 <---> red%28y=2x%2B3%29 is 2 .
The slope of green%282y-x=9%29 <---> green%282y=x%2B9%29 <---> green%28y=%281%2F2%29x%2B9%2F2%29 is 1%2F2 .
That means the two lines intersect at some point P .

That intersection point is part of the Line of Reflection, and
the Line of Reflection is the bisector of the angle formed by the two lines:

Since the slopes of the lines are reciprocals of each other,
the slope of the bisector of that angle is 1 .

We can find the coordinates of P by solving the system formed by the two equations:
system%28y-2x=3%2C2y-x=9%29 ---> system%28x=1%2Cy=5%29 .
So the lines intersect at point 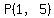P%281%2C5%29 ,
Based on the coordinates of that point,
the equation of the Line of Reflection in point-slope form is
y-5=1%28x-1%29 <---> highlight%28y-5=x-1%29 .
In slope-intercept form, the equation of the Line of Reflection is
y=x-1%2B5 <---> highlight%28y=x%2B4%29 .



NOTES:
Is that the way, you were expected to get to the answer?
Are you expected to name other concepts like "translation", "reflection", "vectors", "matrices" to "show your work"?
Was a different way to the solution expected?

Not convinced that the slope of the Line of Reflection is 1 ?
Here is a concrete example, showing why the slope of the Line of Reflection is 1 .
If the two lines formed the legs of an isosceles triangle ABP,
altitude MP of that triangle would be part of the bisector of angle ABP ,
which is the Line of Reflection we are looking for.
, and M is the midpoint of AB .

How can we find a pair of points A and B to make such an isosceles triangle?
Since the slope of y-2x=3 is 2 ,
we get the coordinates of another point on line y-2x=3
by adding to the coordinates of 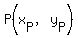P%28x%5BP%5D%2Cy%5BP%5D%29 (1,2), or (2,4), or (3,6), etc.
Let us say that adding (2,4) to the coordinates of P , we get point 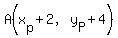A%28x%5Bp%5D%2B2%2Cy%5BP%5D%2B4%29 ,
at a distance sqrt%282%5E2%2B4%5E2%29=sqrt%284%2B16%29=sqrt%2820%29 from the P .
Likewise, since the slope of 2y-x=9 is 1%2F2 adding (4,2) to the coordinates of P ,
we get point B on line 2y-x=9 ,
at the same sqrt%2820%29 distance from P .
To get the coordinates of midpoint M ,
we average the coordinates of A and B ,
So to get to M from P , we add
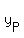"rise" %284%2B2%29%2F2=6%2F2=3 to y%5BP%5D , and
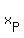"run" %282%2B4%29%2F2=6%2F2=3 to x%5BP%5D .
Since the"rise" and "run" changes in x- and y-coordinates are the same,
the slope of the Line of Reflection is 1 .