Question 1037863: A sector of a circle 7cm subtending an angle 210 at the centre of the circle, is used to form a cone. calculate to the nearest whole number, the base radius of a cone?, height of the cone?, total surface area of a cone?, volume of the cone and vertical angle of the cone
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Is the 7cm measure the radius of the circle? Or is it the diameter?
Assuming the radius is 7cm,
that would be the slant height of the cone
The circumference of the circle measures
  . .
The curved edge of the sector measures  as much as the total circumference, or as much as the total circumference, or
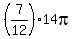   , ,
and that length becomes the circumference of the base of a cone of radius  , so , so
  . .
  ---> --->    (rounded to the nearest whole number). (rounded to the nearest whole number).
A cross section of the cone looks like this triangle:
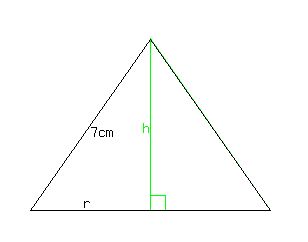 . .
The altitude of length 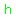 divides the triangle into two right triangles. divides the triangle into two right triangles.
In each of them the legs measure 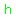 and and  , ,
and the hypotenuse mesures  . .
Using the Pythagorean theorem, and the approximate value  , ,
we can calculate 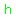 : :




 
So, The height of the cone, to the nearest whole cm is  . .
The surface area of the a whole circle of radius 7cm is
  . .
The surface area of the sector is  as much as the surface area of the a whole circle, or as much as the surface area of the a whole circle, or
    . .
(If you use the approximation  , ,
the area of the a whole circle is calculated as   , ,
and the area of the sector is calculated as   , ,
which is about  ). ).
The surface of the sector becomes the lateral surface of the cone,
so the lateral surface area of the cone is 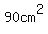 (to the nearest whole number). (to the nearest whole number).
It is not clear from the problem is what is asked for is the total surface area of a cone with those dimensions, or just the lateral area.
The base of the cone, which was not formed out of the sector of the circle,
is a circle of radius  as found above. as found above.
The total surface area of a cone with those dimensions is the lateral surface plus the area of the base.
The area of a circle of radius 4cm is
 (to the nearest whole number), (to the nearest whole number),
so the total surface area for a cone like the one in the problem would be
 . .
The volume of a cone with base radius  and height and height  is is
  (to the nearest whole number). (to the nearest whole number).
The vertical angle can be calculated from the cross section measurements>
 . .  (rounded). (rounded).
From that we get  , ,
and the vertical angle is  . .
So the vertical angle of the cone (in whole degrees is  . .
|
|
|