SOLUTION: Find the value of a for which {{{ f(x)=-2x^3+3(a+2)x^2-12ax+4a^2 }}} is tangent to the positive x-axis and has a relative maximumn at that point of contact.

Algebra ->  Points-lines-and-rays -> SOLUTION: Find the value of a for which {{{ f(x)=-2x^3+3(a+2)x^2-12ax+4a^2 }}} is tangent to the positive x-axis and has a relative maximumn at that point of contact.       Log On


   

Question 1036323: Find the value of a for which +f%28x%29=-2x%5E3%2B3%28a%2B2%29x%5E2-12ax%2B4a%5E2+ is tangent to the positive x-axis and has a relative maximumn at that point of contact.
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
Let (b,0) be the point of tangency.
Now the derivative is given by f'(x) = 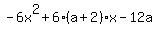-6x%5E2+%2B+6%28a%2B2%29x-12a.
Setting this to 0 to find the critical values, we get x%5E2+-%28a%2B2%29x+%2B+2a+=+%28x-2%29%28x-a%29+=+0.
==> x = 2 or x = a.
Case(i). Let b = a.
==> -2a%5E3%2B3%28a%2B2%29a%5E2-12a%5E2%2B4a%5E2+=+0
==> a%5E2%28a-2%29+=+0, after reduction.
==> a = 0 (double root), or a = 2.
Discard a = 0, because if it is to be the x-coordinate of the point of tangency, a has to be positive. (Remember tangency to positive x-axis.)
==> a = 2.
==> +f%28x%29=-2x%5E3%2B12x%5E2-24x%2B16+=+-2%28x-2%29%5E3+.
But this function has to be discarded as well, because even though f'(2) = 0, f"(2) = 0, and hence there is no maximum at that point, but a point of inflection.

Case (ii). Let b = 2.
==> f%28b=2%29+=+-16%2B3%28a%2B2%29%2A4-24a%2B4a%5E2+=+0
==> 4a%5E2-12a%2B8+=+0
==> a%5E2+-+3a+%2B+2+=+0 ==> (a-1)(a-2) = 0 ==> a = 1 or a = 2.
Now we already know what happens when a = 2, and so we proceed letting a = 1.
==> +f%28x%29=-2x%5E3%2B9x%5E2-12x%2B4+=+%28x-2%29%5E2%28-2x%2B1%29+
By using the 2nd derivative test, we find that there is a relative maximum
at x = 2. (There is relative min at x = 1.)
Therefore highlight%28a+=+1%29.