|
Question 1035907: Find the equations of the lines that pass through point (-1 , 3) and are tangent to the curve  . .
Graph the tangents and the curve
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let (a,b) be a point of tangency at the curve y, and let y - 3 = m(x+1) be the line of tangency passing through (-1,3), where m is the slope of the line.
==>  is the slope of the tangent line. is the slope of the tangent line.
Now y' = 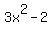 , and the slope of the tangent line at the point of tangency should be m = , and the slope of the tangent line at the point of tangency should be m = 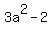 . .
==> 
<==>  <==> <==> 
since (a,b) is a point on the curve.
==>  after simplification. after simplification.
<==> ==> a = 0 or a = -3/2. ==> a = 0 or a = -3/2.
==> b = 1 or b = 5/8, respectively, after substitution.
Thus the two points of tangency are (0,1) and (-3/2,5/8).
==> There are two tangent lines.
The tangent line passing through (0,1) and (-1,3) is  . .
And, the tangent line passing through (-3/2,5/8) and (-1,3) is  . .
|
|
|
| |