SOLUTION: Please help me solve this; Given are two points A(-1,3) and B(3,9).(a) Show that C(5,12)is a point of AB. (b) A Point P(x,y) moves in such a way that AP^2+CP^2=2BP^2. Find the equ

Algebra ->  Points-lines-and-rays -> SOLUTION: Please help me solve this; Given are two points A(-1,3) and B(3,9).(a) Show that C(5,12)is a point of AB. (b) A Point P(x,y) moves in such a way that AP^2+CP^2=2BP^2. Find the equ      Log On


   

Question 1032691: Please help me solve this;
Given are two points A(-1,3) and B(3,9).(a) Show that C(5,12)is a point of AB. (b) A Point P(x,y) moves in such a way that AP^2+CP^2=2BP^2. Find the equation of the locus of P. (c)Show that this locus is a straight line perpendicular to AB.

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
(a) is easy.
A picture is not needed, but I will add a picture so you can visualize it:

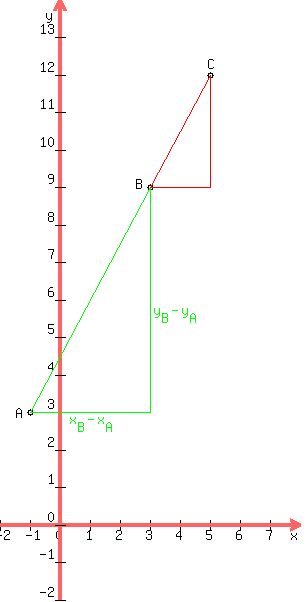
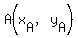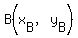Given points A%28x%5BA%5D%2Cy%5BA%5D%29 and B%28x%5BB%5D%2Cy%5BB%5D%29 , the slope of AB is
%28y%5BB%5D-y%5BA%5D%29%2F%28x%5BB%5D-x%5BA%5D%29
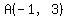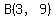For A%28-1%2C3%29 and B%283%2C9%29 , the slope of AB is
%289-3%29%2F%283-%28-1%29%29=6%2F%283%2B1%29=6%2F4=3%2F2 .
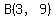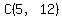For B%283%2C9%29 and C%285%2C12%29 , the slope of BC is
%2812-9%29%2F%285-3%29=3%2F2 .
Since AB and BC have the same slope, they are either parallel or the same line.
As they have point B in common, AB and BC are the same line.

(b) ONE WAY TO GO ABOUT IT (ugly, but probably the expected way):
If point P is 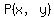P%28x%2Cy%29
,
BP%5E2=%28x-3%29%5E2%2B%28y-9%29%5E2=x%5E2-6x%2B9%2By%5E2-18y%2B81=x%5E2%2By%5E2-6x-18y%2B90 , and
.
So , and
2bP%5E2=2%28x%5E2%2By%5E2-6x-18y%2B90%29=2x%5E2%2B2y%5E2-12x-36y%2B180
So, AP%5E2%2BCP%5E2=2BP%5E2 means
2x%5E2%2B2y%5E2-8x-30y%2B179=2x%5E2%2B2y%5E2-12x-36y%2B180
-8x-30y%2B179=-12x-36y%2B180
12x-8x%2B36y-30y=180-179
4x%2B6y=1
That is the equation of a straight line, which is the locus of P.
Transforming the equation into slope-intercept form, we get
4x%2B6y=1 --> 6y=-4x%2B1 --> y=%28-4x%2B1%29%2F6 --> y=%28-2%2F3x%29%2B1%2F6 .
We could also just find the slope, using a formula.
Either way, the slope of the line is -2%2F3 .
If the product of that slope and the slope of AB (found in part (a) is -1 ,
then the lines are perpendicular, and it so happens that
%28-2%2F3%29%283%2F2%29=-1 , so the locus of P is a line perpendicular to AB.

ANOTHER WAY (possible, depending on what you have already covered in math classes):
When calculating the slopes of AB and BC,
you may have noticed that for points A, B and C
x%5BB%5D-x%5BA%5D=2%28x%5BC%5D-x%5BB%5D%29 and y%5BB%5D-y%5BA%5D=2%28y%5BC%5D-y%5BB%5D%29 .
That tells you that for the distances AB=2BC .
We could calculate those distances, but I only care about their ratios,
so for easier writing, I will rename the distances as BC=c and AB=2c .
You may think of point P as not being on line AB.
However, as it is a moving point, at some point it could be on line AB,
but in that very special case, I would call it point D, and I will say it is a distance d to the other side of A.
I will find d .
The situation would be like this, with the distances:
. (If D is not on the side of A I assumed it to be, d will be a negative value).
Since now P is at D, the equation with the squares is
d%5E2%2B%283c%2Bd%29%5E2=2%282c%2Bd%29%5E2
d%5E2%2B9c%5E2%2B6cd%2Bd%5E2=2%284c%5E2%2B4cd%2Bd%5E2%29
2d%5E2%2B9c%5E2%2B6cd=8c%5E2%2B8cd%2B2d%5E2
9c%5E2%2B6cd=8c%5E2%2B8cd%7D%7D%0D%0A%7B%7B%7B9c%5E2-8c%5E2=8cd-6cd
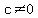c%5E2=2cd and since we know that c%3C%3E0 (even though we did not calculate it), we divide both sides by c and get
c=2d .
Now, what about a point P that is not D?
.
With the Pythagorean theorem (applied to all 3 triangles including side DP), we can easily prove that if P is such that AB and DP are perpendicular, then AP%5E2%2BCP%5E2=2BP%5E2 .
The other way around (proving that if AP%5E2%2BCP%5E2=2BP%5E2 , then AP and DP are perpendicular) I believe requires using the law of cosines, which may be beyond what you have studied.