Question 1029748: Assume quadrilateral ABCD is inscribed in a circle. If  ,  , and  , find x and the measure of angle D.
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Assume quadrilateral ABCD is inscribed in a circle. If , , and , find x and the measure of angle D.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If a quadrilateral is inscribed in a circle, then its opposite angles sum up to 180°.
In other words, If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary.
I think if the teacher gave you this problem, you should be familiar with this fact.
If not, you can read about it in the lesson A property of the angles of a quadrilateral inscribed in a circle in this site.
OK. Based on this fact, you can write an equation for the opposite angles A and C
 =  , or
 =  .
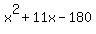Factor left side:
(x-9)*(x+20) = 0.
The only positive root is x = 9.
Hence, angle A is 81° and angle C is 11*9° = 99°. (which is not so important for us now).
What is really important, it is the fact that angle B is 9*9°-2° = 79°.
Then the opposite to B angle D = 180° - 79° = 101°.
Answer. Angle D has the measure of 101°.
|
|
|
