|
Question 102048: Find the slope of any line perpendicular to the line through the points ( 0, 5) and ( -3, -4)
I don't understand this stuff at all.
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! First find the line that goes through those two points. The points are x,y pairsor symbolically (x,y). We'll call (0,5) point 1 and (-3,-4) point 2. The slope of the line is the change in y from point 1 to point 2 divided by the change in x. The change in y is 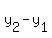 or in your case (-4)-5=-9.The change in x is or in your case (-4)-5=-9.The change in x is 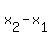 or in your case (-3)-0=-3. The slope,m, of the line is change in y divided by change in x or or in your case (-3)-0=-3. The slope,m, of the line is change in y divided by change in x or



Now you know the slope. A line can be written using the slope-intercept form or


You find b by using either point 1 or point 2 and plugging the values into the equation of the line since both points are on the line. If you use point 1 (0,5), you get


If you use point 2 (-3,-4), you get




You get the same answer.
The line that goes through those two points is :

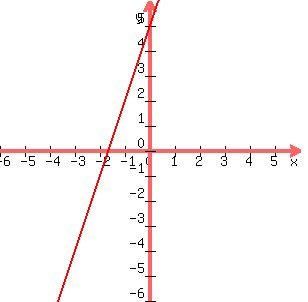
Now that you have your first line, you can find a line that is perpindicular to it. Perpindicular lines have a relationship between their slopes that is:

Their slopes are negative reciprocals of each other. In your case,



Now you have the slope and you can plug it into the slope-intercept form of the line, just like above:


Since you don't have any points that the perpindicular line has to go through, pick a point, (0,0) is usually the easiest, and plug into your line equation.





All you needed was the slope, so

|
|
|
| |