SOLUTION: A(a,-5) and B(2,b) are the endpoints of a diameter, and (1,-1) is the point of trisection nearest to A on this diameter. Find the general form of the equation.

Since (1,-1) is one-third of the way between A(a,-5) and B(2,b),

the distance from (1,-1) to B(2,b) is twice the distance from
A(a,-5) to (1,-1), so we use the distance formula to find this
equation:

    

   

   

   

   

   

   

   

   

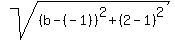
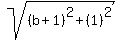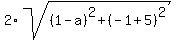
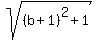
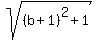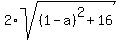
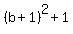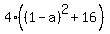
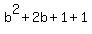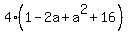
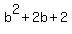
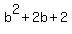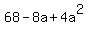
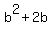We also know that the slope of the line from (1,-1) to B(2,b) is 
equal to the slope of the line from A(a,-5) to (1,-1), because
they are segments of the same line, so we use the slope formula
to get another equation in a and b:

















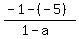
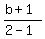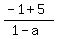
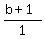
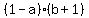
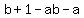
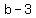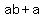
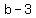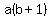
Substitute in







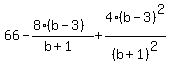Multiply through by the LCD =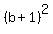 












 
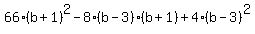
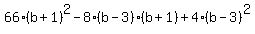
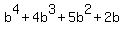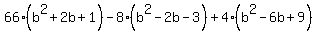
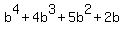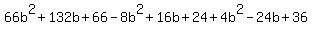
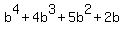
One possible zero is -9

-9 | 1  4 -57 -122 -126
   |   -9  45  108  126
     1 -5 -12  -14    0

So we have factored the polynomial as



A possible zero of the cubic is 7

7 | 1 -5 -12 -14
  |    7  14  14
    1  2   2   0

So we have further factored the polynomial as



The real solutions are b=-9 and b=7

Substitute those in











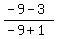
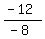
So we have two possibilities to consider

A(1/2,-5) and B(2,7),  A(3/2,-5) and B(2,-9)  

We discard the second one because it is just a
point down below the line y=-5 which is twice
as far from (1,-1) as it is from (1,-1) to
(3/2,5).  But then (1,-1) would then not be a 
point of trisection of AB. So the only points 
to consider for endpoints of the diameter are 

A(1/2,-5) and B(2,7).  

The center of the desired circle is the 
midpoint of AB, which we find by the midpoint
formula:

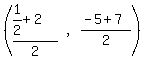(h,k) = 

(h,k) =  

(h,k) =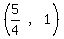 

To find the radius we use the distance formula
from that center to B(2,7) 

r = 

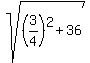r = 

r = 

r = 

r = 

r = 

r = 

r = 

So the standard equation of the circle is  



But the problem asks for the general form, so we must get that in
the form 

You can do that part.  Here's the answer:



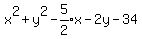Edwin