Question 1010983: find the equation of circle passing through the points of intersection of the lines x + 3y=0 and 2x- 7y = 0 and whose center is point of intersection lines x + y +1=0 and x-2y +4=0
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the equation of circle passing through the points of intersection of the lines


--------------find intersection point


substitute in





=>
intersection point is at ( , , ) )
and whose center is point of intersection lines


----------------------------subtract





then  => => => =>
so, if the center of the circle is at ( , , ) =( ) =( , , ) and circle passes through ( ) and circle passes through ( , , ) , its radius will be the distance between these two points ) , its radius will be the distance between these two points
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (0, 0), we can say (x1, y1) = (0, 0)
So  , , 
Since the second point is (-2, 1), we can also say (x2, y2) = (-2, 1)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (0, 0) and (-2, 1)

 Plug in Plug in  , ,  , ,  , and , and 





==========================================================
Answer:
The distance between the two points (0, 0) and (-2, 1) is exactly  units units
The approximate distance between the two points is about 2.23606797749979 units
So again,
Exact Distance:  units units
Approximate Distance: 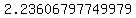 units units
|
so, we have  , , and and  and the equation of your circle is: and the equation of your circle is:



|
|
|