Question 1008377: find standard equation of circle that has centre on the line 5x-2y= -21 and tangent to both co-ordinate axes
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website! STRATEGY: The equivalent linear equation,  must be an equal distance from x-axis, (x,0) as from y-axis, (0,y), because the point on each axis this equal distance is a point of tangency ON EACH of the axes.
Distance from the center (x, (5/2)x+21/2 ) to x-axis and to y-axis must be equal, because each axis contains a tangency point. Use distance formula.
That is a described strategy, but not the actual solution.
Answer by ikleyn(52799)  (Show Source):
You can put this solution on YOUR website! .
find standard equation of a circle that has the center on the line 5x-2y= -21 and tangent to both co-ordinate axes.
---------------------------------------------------------------
Notice that the center of this circle lies on the bisector of the first quadrant angle, which is the line y = x.
So, the center is the intersection point of the straight line 5x - 2y = -21 and the straight line y = x.
In other words, to find the center, we should find the point on the line 5x - 2y = -21 with x = y. It has
the coordinates (a,a) such that 5a - 2a = -21. Hence, 3a = -21 and a = -7. Thus the center is (-7,-7).
Then the equation of the circle is
 =  ,
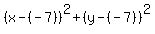or
 =  .
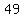It is not the unique solution.
The other solution can be found if another bisector y = -x of the II-IV quadrants is used.
I don't want to go to this matter, but you can, if you want.
|
|
|
