|
Question 1002024: How can i explain how triangles are similar and how do i solve for missing lengths
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Two triangles are 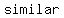 if they have: if they have:
all their angles equal
corresponding sides are in the same ratio
But we don't need to know all three sides and all three angles; two or three out of the six is usually enough.
There are three ways to find if two triangles are similar:
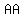 , , 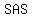 and and 
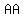 stands for "angle, angle" and means that the triangles have two of their angles equal (could also be called stands for "angle, angle" and means that the triangles have two of their angles equal (could also be called  because when two angles are equal, all three angles must be equal). because when two angles are equal, all three angles must be equal).
If two of their angles are equal, then the third angle must also be equal, because angles of a triangle always add to make  °. °.
example: if one angle is  ° and second angle is ° and second angle is  °, the third °, the third
will be  ° °
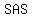 stands for "side, angle, side" and means that we have two triangles where: stands for "side, angle, side" and means that we have two triangles where:
the ratio between two sides is the same as the ratio between another two sides
and we we also know the included angles are equal
If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar.
example:
one pair of sides is in the ratio of 
another pair of sides is in the ratio of 
there is a matching angle of  ° in between them ° in between them
So there is enough information to tell us that the two triangles are similar.
 stands for "side, side, side" and means that we have two triangles with all three pairs of corresponding sides in the same ratio. stands for "side, side, side" and means that we have two triangles with all three pairs of corresponding sides in the same ratio.
If two triangles have three pairs of sides in the 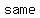 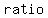 , then the triangles are similar. , then the triangles are similar.
example:
the ratios of sides are:



These ratios are   , so the two triangles are similar. , so the two triangles are similar.
Since the ratios of the lengths of corresponding sides of similar figures are equal, then use this idea to find missing segment lengths in similar figures.
|
|
|
| |