SOLUTION: The sides of a triangle are in the ratio of 4:5:6. Find the size of the largest angle in the triangle.

Algebra ->  Points-lines-and-rays -> SOLUTION: The sides of a triangle are in the ratio of 4:5:6. Find the size of the largest angle in the triangle.      Log On


   

Question 640990: The sides of a triangle are in the ratio of 4:5:6. Find the size of the largest angle in the triangle.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
The sides of a triangle are in the ratio of 4:5:6. Find the size of the largest angle in the triangle. 
The angles will be the same no matter what sides we use, and long as
they are in the ration 4:5:6.  So we may as well take the easiest situation,
which is to assume the sides of the triangle are a=4, b=5 and c=6.

The largest angle C will be opposite the largest sides, c=6, so we use 
the law of cosines for c. We solve for angle C

          c² = a² + b² - 2·a·b·cos(C)

2·a·b·cos(C) = a² + b² - c² 

      cos(C) = 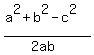%28a%5E2%2Bb%5E2-c%5E2%29%2F%282ab%29

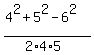      cos(C) = %284%5E2%2B5%5E2-6%5E2%29%2F%282%2A4%2A5%29
 
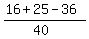      cos(C) = %2816%2B25-36%29%2F%2840%29

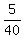      cos(C) = 5%2F40

      cos(C) = 1%2F8

          C = 82.81924422° which I suppose you'd round off to 82.8°


Edwin