|
Question 554458: i need your help please... :
find the point equidistant from (-6,1) and(-1,2) and at a distance 5 from (-2,7).
THANKS!!!
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you need the equation of the line formed by the points (-6,1) and (-1,2).
the equation for this line will be:
y = (1/5)x + 11/5
a graph of this equation looks like this:
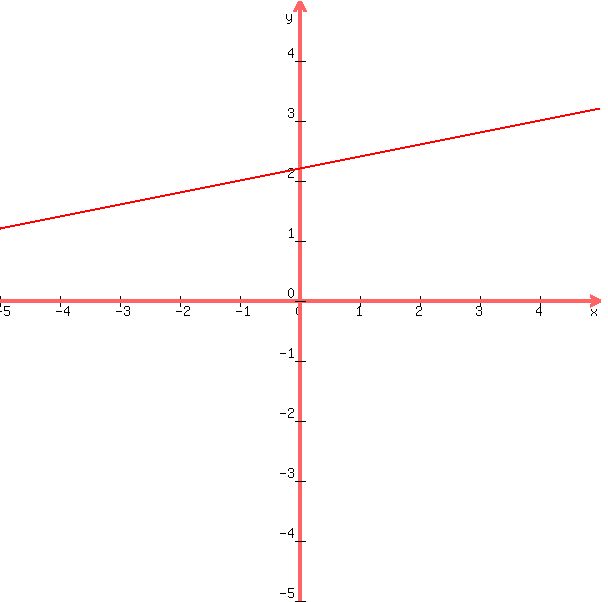
now you need the equation of the line perpendiular to this line and passing through its midpoint.
the midpoint of that line would be the point halfway between (-6,1) and (-1,2)
that point would be:
(-7/2,3/2)
the equation of the line perpendicular to the original line and passing through that point would be:
y = -5x -16
a graph of that line superimposed on the original line looks like this:

all points that are equidistant from the points of (-6,1) and (-1,2) will be on this perpendicular line.
all points 5 units from the point (-2,7) will be on the circumference of the circle that surrounds (-2,7) with a radius of 5 units.
the formula for a circle is:
(x-h)^2 + (y-k)^2 = r^2
the point (h,k) is the center of the circle.
that makes (h,k) = (-2,7) which makes h = -2 and k = 7.
the formula for the circle becomes:
(x+2)^2 + (y-7)^2 = r^2
since the radius of the circle has to be 5, then r = 5 and r^2 = 25.
the equation for the circle becomes:
(x+2)^2 + (y-7)^2 = 25
to graph this equation, solve for y to get:
y = +/- sqrt(25-(x+2)^2) + 7
the graph of this equation, superimposed on the graph of the other 2 lines, will look like this:

it appears there are 2 points that will satisfy the equation.
those points are the intersection of the line perpendicular to the original line and the circumference of the circle.
a picture of the final graph with the relationships drawn out is shown below:

the point (-5.34,10.72) is 9.74 units from (-6,1) and (-1,2) and is also 5 units away from (-2,7).
the point (-3.66,2.28) is 2.67 units away from (-6,1) and (-1,2) and is also 5 units away from (-2,7).
both the points (-5.34,10.72) and (-3.66,2.28) are on the circumference of the circle and on the line perpendicular to the original line and intersecting halfway between the points (-6,1) and (-1,2).
the points (-3.66,2.28) and -5.34,10.72) have been rounded to 2 decimal places.
those are the solutions to the problem.
the solution is 2 points rather than just 1.
|
|
|
| |