SOLUTION: I am not sure how to find the length and width of a rectangle, by looking at the perimeter and area. The question is "A rectangle has an area of 35 sq. ft, and a perimeter of 27 f

Algebra ->  Points-lines-and-rays -> SOLUTION: I am not sure how to find the length and width of a rectangle, by looking at the perimeter and area. The question is "A rectangle has an area of 35 sq. ft, and a perimeter of 27 f      Log On


   

Question 171474: I am not sure how to find the length and width of a rectangle, by looking at the perimeter and area. The question is "A rectangle has an area of 35 sq. ft, and a perimeter of 27 ft. What is the length and width of the rectangle?"
hope you can help!! thank you.
Found 3 solutions by monika_p, josmiceli, jojo14344:
Answer by monika_p(71) About Me  (Show Source):
You can put this solution on YOUR website!
Formula for area of rectangle is A= a*b
Formula for perimeter of rectangle is P=2a+2b
where a and b are the sides of rectangle
You have given A=35sq ft and P= 27 ft, then
a*b = 35
2a+2b = 27
Now solve system of two equations
From first equation we have a=35/b,
then second equation:
2*(35/b) +2b =27 , now multiply both sides by b
2*35 +2b^2=27b
2b^2-27b+70=0 quadratic equation (Ax^2+Bx+C=0)
A=2, B=-27, C=70
find discriminant B^2-4AC = 169 > 0 equation has 2 solutions
b1=%28-B-sqrt%28B%5E2-4AC%29%29%2F%282A%29
b1=3.5
b2=%28-B%2Bsqrt%28B%5E2-4AC%29%29%2F%282A%29
b2=10

a = 35/b then for b1=3.5 ---> a1=10 and for b2=10---> a2=3.5
We got set of two the same numbers then lets a=10ft and b=3.5ft
Prove : A = 10*3.5 =35 and P= 2*10+2*3.5=27

Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
First, choose symbols for the width and length
width = w
length = l
The area of the rectangle is A+=+w%2Al
The problem gives me A+=+35ft2, so
35+=+w%2Al
The formula for the perimeter is obtained by
adding up the lengths of the 4 sides, knowing
that the opposite sides are equal
P+=+w+%2B+w+%2B+l+%2B+l
P+=+2w+%2B+2l
The problem gives me P+=+27ft, so
27+=+2w+%2B+2l
Now I've got 2 equations and 2 unknowns, so they're
solvable
35+=+w%2Al
divide both sides by w
l+=+35%2Fw
Now substitute
27+=+2w+%2B+2%2A%2835%2Fw%29
Multiply both sides by w
27w+=+2w%5E2+%2B+70
2w%5E2+-+27w+%2B+70+=+0
Use the quadratic equation to solve
w+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
where
a+=+2
b+=+-27
c+=+70
w+=+%28-%28-27%29+%2B-+sqrt%28+%28-27%29%5E2-4%2A2%2A70+%29%29%2F%282%2A2%29+
w+=+%2827+%2B-+sqrt%28729+-+560%29%29%2F4+
w+=+%2827+%2B-+sqrt%28169%29%29%2F4+
w+=+%2827+%2B+13%29%2F4
w+=+10
and also
w+=+%2827+-+13%29%2F4
w+=+7%2F2
w+=+3.5
Now which answer makes sense?
If w+=+10
35+=+10%2Al
l+=+3.5
Does the perimeter = 27?
27+=+2%2A10+%2B+2%2A3.5
27+=+20+%2B+7
OK
The other answer works, too, and is more
appropriate since it makes the width shorter
w+=+3.5
l+=+10

Answer by jojo14344(1513) About Me  (Show Source):
You can put this solution on YOUR website!

A=L%2AW , EQN 1
we get,
35ft%5E2=L%2AW ---> L=35%2FW, EQN 2
Also,
P=2L%2B2W, subst. EQN 2,
27=2%2835%2FW%29%2B2W
27=70%2FW%2B2W ---> 27=%2870%2B2W%5E2%29%2FW
27W=70%2B2W%5E2 ---> follows a quadratic eqn:2W%5E2-27W%2B70=0
where ---->system%28a=2%2Cb=-27%2Cc=70%29
note:w=x

x=%2827%2B-sqrt%28729-560%29%29%2F4=%2827%2B-sqrt%28169%29%29%2F4=%2827%2B-13%29%2F4
2 values:
x=%2827%2B13%29%2F4=40%2F4=10ft, or
x=%2827-13%29%2F4=14%2F4=3.5ft
Width (either/or)---->system%28W%5B1%5D=10ft%2CW%5B2%5D=3.5ft%29
For Length, as per EQN 2:
L=35%2F10=3.5ft
L=35%2F3.5=10ft
LENGTH (either/or)---->system%28L%5B1%5D=3.5ft%2CL%5B2%5D=10ft%29
We'll check using: 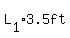L%5B1%5D3.5ft & W%5B1%5D=10ft:
A=L%2AW
35ft%5E2=%283.5ft%29%2810ft%29
35ft%5E2=35ft%5E2, good
P=2%28L%2BW%29
27ft=2%283.5%2B10%29
27ft=2%2813.5ft%29
27ft=27ft, good
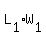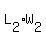*Note: either you use L%5B1%5D%2AW%5B1%5D or L%5B2%5DW%5B2%5D will just be the same. Same thing on the Perimeter
Thank you,
Jojo