|
Question 1207455: ABC is a triangle with ∠CAB=15
∘
and ∠ABC=30
∘
. If M is the midpoint of AB, Sin then ∠ACM= ?
Found 3 solutions by greenestamps, Edwin McCravy, ikleyn:
Answer by greenestamps(13219)   (Show Source): (Show Source):
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
ABC is a triangle with ∠CAB=15∘ and ∠ABC=30∘.
If M is the midpoint of AB, find ∠ACM.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution by Edwin is perfect and deserves admiration.
My congratulations to Edwin with this great achievement.
I came to bring a shorter solution.
The given part is shown in Figure 1 below.
 Figure 1.
Triangle ABC has the angles A= 15°, B= 30° and C= 180°-15°-30°= 135°.
We want to find angle
Figure 1.
Triangle ABC has the angles A= 15°, B= 30° and C= 180°-15°-30°= 135°.
We want to find angle  .
Draw perpendicular CH from vertex C to the base AB (Figure 2). .
Draw perpendicular CH from vertex C to the base AB (Figure 2).
 Figure 2.
First part of the solution is the same as that of Edwin' solution,
and it shows that a =
Figure 2.
First part of the solution is the same as that of Edwin' solution,
and it shows that a =  , b = , b =  .
The rest of the solution is different (very simple and totally geometrical).
Triangle BHC is a right-angled triangle with the acute angle B of 30°.
Hence, the opposite leg CH is half of the hypotenuse BC
CH = .
The rest of the solution is different (very simple and totally geometrical).
Triangle BHC is a right-angled triangle with the acute angle B of 30°.
Hence, the opposite leg CH is half of the hypotenuse BC
CH =  = = 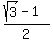 , (1)
while its other leg BH is , (1)
while its other leg BH is  times the hypotenuse BC
BH = times the hypotenuse BC
BH = 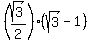 = = 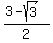 .
Then the segment MH is the complement of BH to 1
MH = 1 - .
Then the segment MH is the complement of BH to 1
MH = 1 - 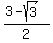 = =  = = 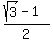 . (2)
Comparing expressions (1) and (2), we see that CH = MH.
Hence, right-angled triangle MHC is isosceles right-angled triangle,
which implies that angle MCH is 45°.
Thus ∠ACM = 135° - 60° - 45° = 30°,
and the problem is solved completely. . (2)
Comparing expressions (1) and (2), we see that CH = MH.
Hence, right-angled triangle MHC is isosceles right-angled triangle,
which implies that angle MCH is 45°.
Thus ∠ACM = 135° - 60° - 45° = 30°,
and the problem is solved completely.
|
|
|
| |