|
Question 1204896: The segment joining (-2,-3), (6,1) is extended each way a distance equal to one-fourth its own length. Find the terminal points.
Found 2 solutions by mananth, math_tutor2020:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! The segment joining (-2,-3), (6,1) is extended each way a distance equal to one-fourth its own length. Find the terminal points.
The distance between A(-2,-3),B (6,1) is
AB = 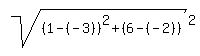 =24 =24
Let C(x1,y1) be the point extended on side of A by 6 units. (1/4)*24=6
Section formula for internal division
P=(((mx2+nx1)/(m+n)),((my2+ny1)/(m+n)))
m and n is the ratio of division
B divides AD in the ratio of 4:1
6=4*x2+1*(-2))/ (4+1)
x1=8
-1= (1*(-3))+4(y1)/(4+1)
y1=2
D(8,2)
In Segment ABC A divides CB in the ratio of 1:4
-2=( (4*x1+1*(6))/(4+1)
solve
x1=-4
-3= (4)*(y2)+(1)(1)))/(4+1)=-4
y1=-4
C(-4,-4)
 . .
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A = (-2, -3)
B = (6, 1)
The horizontal gap from A to B is 8 units.
Use a number line to see there are 8 spaces between -2 and 6.
Or subtract and use absolute value:  or or 
Absolute value is needed since a negative distance isn't valid.
One quarter of this 8 unit horizontal gap is 8/4 = 2 units.
Let p = 2
The vertical gap from A to B is 4 units.
One quarter of which is 4/4 = 1.
Let q = 1.
When starting at A(-2,-3), move p = 2 units left and q = 1 unit down.
This has us arrive at C(-4,-4) as shown in the tutor @mananth's diagram
Now focus on point B(6,1)
We move p = 2 units right and q = 1 unit up to arrive at D(8,2).
Refer to that same diagram.
In summary, segment AB extends out to CD such that
A = (-2, -3)
B = (6, 1)
C = (-4,-4)
D = (8,2)
GeoGebra is a very useful tool to confirm the answers.
Side notes:
AB = 4*AC
AB = 4*BD
CD = (3/2)*AB
|
|
|
| |