SOLUTION: A line through (-1,b) and (c,8) is parallel to a line through (-6,3) and (0,12) Find. The values of b and c that make the statement true.

Algebra ->  Points-lines-and-rays -> SOLUTION: A line through (-1,b) and (c,8) is parallel to a line through (-6,3) and (0,12) Find. The values of b and c that make the statement true.      Log On


   

Question 1099454: A line through (-1,b) and (c,8) is parallel to a line through (-6,3) and (0,12) Find. The values of b and c that make the statement true.
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Here's the line through (-6,3) and (0,12)



We use the fact that parallel lines have the same slope.

m%22%22=%22%22%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29
where (x1,y1) = (-1,b)
and where (x2,y2) = (c,8)

m%22%22=%22%22%288-b%29%2F%28c-%28-1%29%29
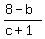m%22%22=%22%22%288-b%29%2F%28c%2B1%29

That must equal the slope of the line though (-6,8) and (0,12)


m%22%22=%22%22%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29
where (x1,y1) = (-6,3)
and where (x2,y2) = (0,12)

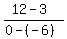
m%22%22=%22%22%2812-3%29%2F%280-%28-6%29%29
m%22%22=%22%229%2F6
m%22%22=%22%223%2F2

So we set the slopes equal.

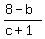
%288-b%29%2F%28c%2B1%29%22%22=%22%223%2F2

There are an infinite number of possible answers for that

b = -7, c = 9 the line through (-1,-7) and (9,8).
b = -4, c = 7 the line through (-1,-4) and (7,8).
b = -1, c = 5 the line through (-1,-1) and (5,8).
b = 2, c = 3 the line through (-1,2) and (3,8).
b = 5, c = 1 the line through (-1,5) and (1,8).
b = 11, c = -3 the line through (-1,11) and (-3,8).

Here are the graphs of those solutions.  There are trillions
more.  Did your teacher warn you that there are many many different
solutions to this problem?



Edwin