Tutors Answer Your Questions about Exponential-and-logarithmic-functions (FREE)
Question 1181507: Determine the absolute deviation and the coefficient of variation.
𝑦=[200.432 (±0.002)]^1/2 / log(20.42 × 10^15(±0.06))
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate the absolute deviation and coefficient of variation for the given expression:
**1. Calculate the value of y:**
y = sqrt(200.432) / log(20.42 × 10^15)
y ≈ 14.157 / 15.310
y ≈ 0.9246
**2. Calculate the uncertainty in y:**
To do this properly, we need to consider the uncertainties in both the numerator and the denominator. We'll use the formula for propagation of uncertainty through division:
(δy/y) = sqrt((δA/A)^2 + (δB/B)^2)
Where:
* A = 200.432, δA = 0.002
* B = 20.42 × 10^15, δB = 0.06 × 10^15
First, find the relative uncertainties:
* (δA/A) = 0.002 / 200.432 ≈ 0.00001
* (δB/B) = 0.06 × 10^15 / (20.42 × 10^15) ≈ 0.00294
Now, calculate the relative uncertainty in y:
(δy/y) = sqrt((0.00001)^2 + (0.00294)^2)
(δy/y) ≈ 0.00294
Finally, calculate the absolute uncertainty in y:
δy = (δy/y) * y
δy ≈ 0.00294 * 0.9246
δy ≈ 0.00272
**3. Express the result:**
y = 0.9246 ± 0.00272
**4. Calculate the coefficient of variation:**
Coefficient of variation = (δy / y) * 100%
Coefficient of variation = (0.00272 / 0.9246) * 100%
Coefficient of variation ≈ 0.294%
**Therefore:**
* **Absolute deviation:** ± 0.00272
* **Coefficient of variation:** ≈ 0.294%
Question 1209412: Find all real numbers x such that (3x - 27)^3 + (27x - 3)^3 = (3x + 27x - 30)^3.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Question 1198664: An optical instrument with limiting magnitude L of any optical telescope and lens
diameter D, in inches, is given by
𝐿 = 8.8 + 5.1 𝑙𝑜𝑔 𝐷
a) Determine the limiting magnitude for a homemade I -inch reflecting telescope.
b) Determine the diameter of a lens that would have a limiting magnitude of R.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Determine the limiting magnitude for a homemade 1-inch reflecting telescope.**
* Use the given formula: L = 8.8 + 5.1 * log(D)
* Substitute D = 1 inch:
L = 8.8 + 5.1 * log(1)
* Since log(1) = 0:
L = 8.8 + 5.1 * 0
L = 8.8
**Therefore, the limiting magnitude for a homemade 1-inch reflecting telescope is 8.8.**
**b) Determine the diameter of a lens that would have a limiting magnitude of R.**
* **Rearrange the formula to solve for D:**
* L = 8.8 + 5.1 * log(D)
* L - 8.8 = 5.1 * log(D)
* (L - 8.8) / 5.1 = log(D)
* 10^[(L - 8.8) / 5.1] = 10^(log(D))
* 10^[(L - 8.8) / 5.1] = D
**Therefore, the diameter of a lens that would have a limiting magnitude of R is:**
* D = 10^[(R - 8.8) / 5.1]
This equation allows you to calculate the required lens diameter for any desired limiting magnitude (R).
Question 1209241: Can you explain the quotient rule and the power rule and how to tell the difference between them in example. I’m confused how you know the difference and what they mean by the power rule.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Can you explain the quotient rule and the power rule and how to tell the difference between
them in example. I’m confused how you know the difference and what they mean by the power rule.
~~~~~~~~~~~~~~~~~~~~~~
It seems to me that you want to ask something different,
but your question drowned in words.
A reasonable question to ask is THIS:
Let's consider a rational function y(x) = 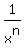 , where n is a positive integer number.
We can consider it as a power function y = , where n is a positive integer number.
We can consider it as a power function y = 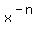 , too.
If we want to find the derivative y'(x), we can do it using the power rule
or using the quotient rule.
Is there the difference and how to know, which rule to use ? , too.
If we want to find the derivative y'(x), we can do it using the power rule
or using the quotient rule.
Is there the difference and how to know, which rule to use ?
The answer is that both these rules lead to the same result in this case,
so one can use any of these two rules.
Indeed, if we use the power rule, then
y'(x) = 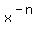 ' = ' = 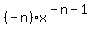 = = 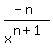 . (1)
If we use the quotient rule, then the calculations are as follows
(derivative of the numerator)*denominator - numerator*(derivative of denominator)
y' = ----------------------------------------------------------------------------------- =
denominator^2
0*denominator - 1*n*x^(n-1) (-n)
= ------------------------------ = --------- (2)
x^(2n) x^(n+1)
(1) and (2) are the same, so the answer is the same:
you may use any of these two rules/techniques, the result is the same. . (1)
If we use the quotient rule, then the calculations are as follows
(derivative of the numerator)*denominator - numerator*(derivative of denominator)
y' = ----------------------------------------------------------------------------------- =
denominator^2
0*denominator - 1*n*x^(n-1) (-n)
= ------------------------------ = --------- (2)
x^(2n) x^(n+1)
(1) and (2) are the same, so the answer is the same:
you may use any of these two rules/techniques, the result is the same.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Question 1209240: A biologist is researching a newly discovered species of bacteria. At time T equals zero hours, he put 100 bacteria into what he has determined to be a favorable growth medium. Six hours later, he measures 450 bacteria. Assuming exponential growth, what is the growth constant K for the bacteria? (Round K2 decimal places) By what hour to the nearest 10 will there be 1000 bacteria?
Answer by timofer(105)  (Show Source): (Show Source):
Question 1208791: Solve for x.
12^(sqrt{x^2}) - 24^(x - 2) = 144
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve for x.
12^(sqrt{x^2}) - 24^(x - 2) = 144
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It is not for algebraic solution - in Algebra, there are no methods solving such equations.
Use either your graphics calculator or online tools to get approximate numerical solutions.
For example, you may use an online solver https://www.desmos.com/calculator
Print there y = 12^(sqrt{x^2}) - 24^(x - 2) in one window and y = 144 in another window.
Calculator will provide the plot, and you can identify two root
x = -2 (an approximate value) and x = 2.00281 (another approximate value)
by clicking at the intersection points. ANSWER
Solved.
Question 1208832: Investing $8,000 for 6 years.
Option #1
7% compounded monthly
Option #2
6.85% compounded continuously
Which is the better investment?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52790)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Option 1
A = P*(1+r/n)^(n*t)
A = 8000*(1+0.07/12)^(12*6)
A = 12160.84 approximately when rounding to the nearest penny
Option 2
A = P*e^(r*t) where e = 2.718 roughly
A = 8000*e^(0.0685*6)
A = 12066.60 approximately when rounding to the nearest penny
You earn slightly more with option 1.
The difference is 12160.84 - 12066.60 = 94.24 extra dollars.
Question 1208790: Solve for x.
5^(x + 2) + 6^x = 30
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is not for algebraic solution - in Algebra, there are no methods solving such equations.
Use either your graphics calculator or online tools to get approximate numerical solutions.
For example, you may use an online solver https://www.desmos.com/calculator
Print there y = 5^(x + 2) + 6^x in one window and y = 30 in the second window
Calculator will provide the plot, and you can identify the root x = 0.08852 there
as the intersection point of the two graphs (an approximate value). ANSWER
Solved.
Question 1208811: Solve for x.
5^(sin x) - 5x + 10 = 0
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is not for algebraic solution - in Algebra, there are no methods solving such equations.
Use either your graphics calculator or online tools to get approximate numerical solutions.
For example, you may use an online solver https://www.desmos.com/calculator
Print there y = 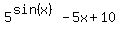 .
Calculator will provide the plot, and you can identify the root x = -2.04787 there (an approximate value). ANSWER .
Calculator will provide the plot, and you can identify the root x = -2.04787 there (an approximate value). ANSWER
Solved.
Question 1208812: Solve for x.
12^(sin x + cos x) + 24x^2 = 0
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
ANSWER: No solution
The expression 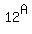 is greater than zero for any expression A; the expression is greater than zero for any expression A; the expression 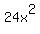 is always zero or positive. So the sum of the two expressions is always greater than zero. is always zero or positive. So the sum of the two expressions is always greater than zero.
Question 1208755: Find the range of y = e^x.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1208756: Find the range of y = log[sqrt{e}].
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1208757: Find the range of y = [[ 2x ]].
Note: [[ 2x ]] is a step function.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
"[[A]]" is a standard representation of the floor (greatest integer in) function. If you intended it to be something different, you need to define it.
The floor function always returns an integer value; and there is no restriction on how large or small that integer might be. So
ANSWER: the range of [[2x]] is the set of all integers.
Question 1208600: Bismuth-210 is an isotope that radioactively decays by about 13% each day, meaning 13% of the remaining Bismuth-210 transforms into another atom (polonium-210 in this case) each day. If you begin with 215 mg of Bismuth-210, how much remains after 7 days?
After 7 days, mg of Bismouth-210 remains.
Round your answer to the nearest hundredth as needed.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 81.11 mg
Work Shown
P = 215 mg is the starting amount
r = 0.13 is the decimal form of the decay rate
t = 7 days
A = P*(1-r)^t ............... exponential decay equation
A = 215*(1-0.13)^7
A = 81.109780898733
A = 81.11 mg
The 210 is never used since it's part of the name, rather than an amount.
Some teachers love to place red herrings to distract students.
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Bismuth-210 is an isotope that radioactively decays by about 13% each day, meaning 13% of the remaining Bismuth-210
transforms into another atom (polonium-210 in this case) each day. If you begin with 215 mg of Bismuth-210, how much remains after 7 days?
After 7 days, mg of Bismouth-210 remains.
Round your answer to the nearest hundredth as needed.
~~~~~~~~~~~~~~~~~~~~
The remaining mass of the Bismuth-210 after 1 day is 215*(1-0.13) = 215*0.87 mg.
The remaining mass of the Bismuth-210 after 2 days is 215*0.87*0.87 = 215*0.87^2 mg.
The remaining mass of the Bismuth-210 after 3 days is 215*0.87^2*0.87 = 215*0.87^3 mg.
. . . . . and so on . . . . .
The remaining mass of the Bismuth-210 after 7 days is 215*0.87^6*0.87 = 215*0.87^7 = 81.10978 mg (rounded). ANSWER
Solved, with explanations.
Question 1208301: Hi can you help please:
int (3 x^3) (sqrt(16-x^2)) dx
Just not sure if my trig substitutions are working
Found 3 solutions by mccravyedwin, math_tutor2020, Edwin McCravy:
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Question 1208258: Hi, can you help me with part b please:
A particle is oscillating in Simple Harmonic Motion and is 𝑥 metres away from the origin after 𝑡 seconds. The movement of the particle can be modelled with the equation 𝑥 = 2 cos(3𝑡 + 𝛼)
a) Prove that its acceleration is −9𝑥 𝑚𝑠^-2.
b) If initially, 𝑥 = 1𝑚 with velocity 3√3 𝑚𝑠^-1, find a suitable value for 𝛼.
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hi, can you help me with part b please:
A particle is oscillating in Simple Harmonic Motion and is 𝑥 metres away from the origin after 𝑡 seconds.
The movement of the particle can be modelled with the equation 𝑥 = 2 cos(3𝑡 + 𝛼)
a) Prove that its acceleration is −9𝑥 𝑚𝑠^-2.
b) If initially, 𝑥 = 1𝑚 with velocity 3√3 𝑚𝑠^-1, find a suitable value for 𝛼.
~~~~~~~~~~~~~~~~~~~
Since you ask about part (b) only, I will focus on it.
We are given that initially x= 1 m. The term "initially" means "at t= 0".
It gives this equation
2cos(a) = 1,
cos(a) =  ,
a = ,
a =  or a = or a =  . (1)
We also are given that "initially" velocity is . (1)
We also are given that "initially" velocity is  m/s.
Velocity is the first derivative of the position function with respect to time,
so this condition leads to this equation m/s.
Velocity is the first derivative of the position function with respect to time,
so this condition leads to this equation
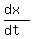 = =  at t= 0,
or
-2*3sin(3t+a) = at t= 0,
or
-2*3sin(3t+a) =  at t= 0,
sin(3t+a) = at t= 0,
sin(3t+a) =  at t= 0,
or
sin(a) = at t= 0,
or
sin(a) =  .
a = .
a =  or a = or a =  . (2)
Comparing (1) and (2), we conclude that
a = . (2)
Comparing (1) and (2), we conclude that
a =  .
At this point, the solution is complete and the answer is achieved.
ANSWER. A suitable value of "a" is a = .
At this point, the solution is complete and the answer is achieved.
ANSWER. A suitable value of "a" is a =  .
Surely, you can add .
Surely, you can add  to it, k = 0, +/-1, +/-2, . . . , if you want. to it, k = 0, +/-1, +/-2, . . . , if you want.
Solved, answered and explained.
Question 1208255: Hi, can you help with this question:
Use x=alphasintheta for sqrt(alpha^2-x^2), x= alphatantheta for sqrt(alpha^2+x^2) and x= alphasectheta for sqrt(x^2-alpha^2), to find int (x/(sqrt(1-x^2)^3) dx
Found 2 solutions by math_tutor2020, Edwin McCravy:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I don't understand the stuff in the beginning, so I skipped on over
to find int (x/(sqrt(1-x^2)^3) dx
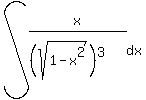
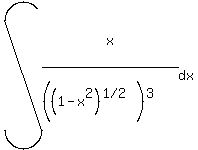
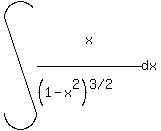
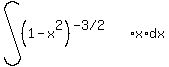 Students nowadays do lots more u substituting than they did in
the old days when I was teaching. We taught "putting in and taking out",
which meant:
"Putting in a factor to cause an expression to become the differential
and offsetting by multiplying on the outside of the integral by its reciprocal."
We would think of, not write, the power rule
Students nowadays do lots more u substituting than they did in
the old days when I was teaching. We taught "putting in and taking out",
which meant:
"Putting in a factor to cause an expression to become the differential
and offsetting by multiplying on the outside of the integral by its reciprocal."
We would think of, not write, the power rule  ,
adding 1 to the exponent and dividing by it.
You need to have an expression for u, a du, and a constant for an exponent.
So for this: ,
adding 1 to the exponent and dividing by it.
You need to have an expression for u, a du, and a constant for an exponent.
So for this:
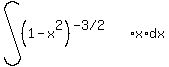 Then we'd think, not write, "u is (1-x2).
Then we'd think, not write, "we need to get a du".
We would observe that the differential of 1-x2 was -2x*dx, and that
we could easily make the x become -2x by multiplying x by -2 and multiplying on
the outside of the integral by the reciprocal of -2 which
is -1/2. That would give us our du. So we'd write this:
Then we'd think, not write, "u is (1-x2).
Then we'd think, not write, "we need to get a du".
We would observe that the differential of 1-x2 was -2x*dx, and that
we could easily make the x become -2x by multiplying x by -2 and multiplying on
the outside of the integral by the reciprocal of -2 which
is -1/2. That would give us our du. So we'd write this:
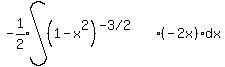 So we'd think, not write, "u is 1-x2 and the (-2x)dx is du,
and then we'd think of the power rule of adding 1 to the exponent and then
dividing by it.
So we'd add 1 to -3/2 and get -1/2
Then we'd divide by the -1/2 and realize that it would cancel with the -1/2
we just put on the outside of the integral (to offset the multiplication by -2) and we'd get
So we'd think, not write, "u is 1-x2 and the (-2x)dx is du,
and then we'd think of the power rule of adding 1 to the exponent and then
dividing by it.
So we'd add 1 to -3/2 and get -1/2
Then we'd divide by the -1/2 and realize that it would cancel with the -1/2
we just put on the outside of the integral (to offset the multiplication by -2) and we'd get
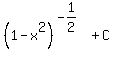 and then and then
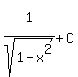 Now if that's too hard for you and you want to do all the substituting that they
are requiring today, go to
https://www.integral-calculator.com/
and they'll go through it step by step for you.
Edwin
Now if that's too hard for you and you want to do all the substituting that they
are requiring today, go to
https://www.integral-calculator.com/
and they'll go through it step by step for you.
Edwin
Question 1208235: log[5](x-2)=3 logarithm to exponential form
Found 2 solutions by math_tutor2020, mananth:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1207550: Please help me solve the equation f(𝓍) = -log⅓ 3√𝓍 :
→ f(𝓍) = -log⅓ 3√𝓍
→ f(𝓍) = - ⅓ log⅓ 𝓍
→ f(𝓍) = ⅓ log3 𝓍
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Question 1207490: \(5^{(}logx-1)/125=(1/5)^{(}logx)^{2}-logx\)
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I was just going to post Ikleyn's solution before she posted it. I had tried
another version of what you notation might mean and finally stumbled onto
the same one she interpreted it to be. I am unfamiliar with that notation as
things like {(} and backward slashes \ are foreign to me. What notation is that?
I've seen it elsewhere.
Edwin
Answer by ikleyn(52790)   (Show Source): (Show Source):
Question 1207302: The lengths of the sides of an equilateral triangle are log4(a), log10(b), log25(a+b) where A and B are positive numbers. What is the value of a/b?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The lengths of the sides of an equilateral triangle are log4(a), log10(b), log25(a+b)
where A and B are positive numbers. What is the value of a/b?
~~~~~~~~~~~~~~~
We are given
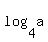 = = 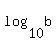 = = 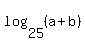 .
Let k = .
Let k = 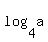 = = 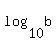 = = 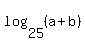 .
It means that .
It means that
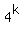 = a, (1) = a, (1)
 = b, (2) = b, (2)
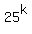 = a + b. (3)
It implies that = a + b. (3)
It implies that
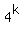 + +  = = 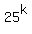 .
Divide both sides (all the terms) by .
Divide both sides (all the terms) by 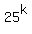 . You will get . You will get
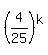 + + 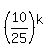 = 1,
or = 1,
or
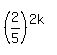 + + 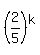 = 1. (4)
Let x = = 1. (4)
Let x = 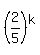 . Then equation (4) takes the form . Then equation (4) takes the form
 + x = 1,
or + x = 1,
or
 + x - 1 = 0.
Its roots are + x - 1 = 0.
Its roots are  = = 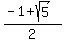 , ,  = = 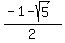 .
Our value of x is positive .
Our value of x is positive 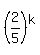 ; so, we consider only positive root x = ; so, we consider only positive root x =  .
Thus we have .
Thus we have
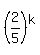 = =  ,
or ,
or
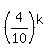 = =  .
But from (1) and (2), .
But from (1) and (2),  = = 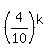 .
Thus we proved that .
Thus we proved that  = =  .
ANSWER. .
ANSWER.  = =  = 0.618033989 (approximately). = 0.618033989 (approximately).
Solved.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1207158: Log4x+log4(x-3)=1 find the solution
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52790)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Question 1206983: how long would it take for 1000 deposited in an account payinv 6% interest compounded countinously to earn 200 interest
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
how long would it take for 1000 deposited in an account payinv 6% interest
compounded countinously to earn 200 interest
~~~~~~~~~~~~~~~~~~~
Formula for the future value of a continuously compounded account in this problem is
FV = 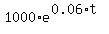 ,
where "t" is in years, "e" is the base of natural logarithms.
So, we write for the total
1000 + 200 = ,
where "t" is in years, "e" is the base of natural logarithms.
So, we write for the total
1000 + 200 = 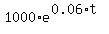 or
1200 =
or
1200 = 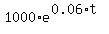 .
Now we solve this equation, step by step, and find time "t". .
Now we solve this equation, step by step, and find time "t".
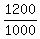 = =  1.2 = =
1.2 = =  Next, take the natural logarithm of both sides
ln(1.2) = 0.06*t
t =
Next, take the natural logarithm of both sides
ln(1.2) = 0.06*t
t = 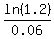 = 3.038692613
So, the ANSWER is that the time to earn 200 interest is about 3 years.
(More precisely, 3 years and 15 days). = 3.038692613
So, the ANSWER is that the time to earn 200 interest is about 3 years.
(More precisely, 3 years and 15 days).
Solved.
-----------------
To see many other similar (and different) solved problems on continuously compounded accounts, look into the lesson
- Problems on continuously compound accounts
in this site.
After reading this lesson, you will tackle such problems on your own without asking for help from outside.
Question 1206952: a^3 - b^2 = 11
a^2 + b = 13
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  .....eq.1 .....eq.1
 ....eq.2 ....eq.2
---------------------
start with
 ....eq.2, solve for ....eq.2, solve for 
 ....eq.1a ....eq.1a
go to eq.2, substitute 
 .....eq.1 .....eq.1



 ....factor ....factor

real solutions:
 => => 
 , using calculator we get , using calculator we get  ≈ ≈
go to
 ....eq.1a, substitute ....eq.1a, substitute 




 ≈ ≈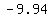
complex solutions: using calculator
 ≈ ≈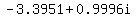 , ,  ≈ ≈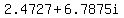
 ≈ ≈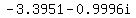 , ,  ≈ ≈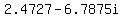
answer:
 , ,
 ≈ ≈ , , ≈ ≈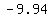
 ≈ ≈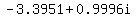 , ,  ≈ ≈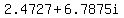
 ≈ ≈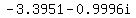 , ,  ≈ ≈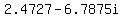

Question 1206832: The population of a colony of rabbits grows exponentially. The colony begins with 5 rabbits; 5 years later there are 320 rabbits.
(a) estimate how long it takes for the population of rabbits to reach 1000 rabbits.
Found 3 solutions by Edwin McCravy, MathLover1, josgarithmetic:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by josgarithmetic(39618)  (Show Source): (Show Source):
Question 1206651: The population of J-Town in 2019 was estimated to be 76,500 people with an annual rate of increase of 2.4%.
Part A. Write an equation to model future growth.
Part B. What is the growth factor for J-Town?
Part C. Use the equation to estimate the population in 2072 to the nearest hundred people.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The population of J-Town in 2019 was estimated to be 76,500 people with an annual rate of increase of 2.4%.
Part A. Write an equation to model future growth.
Part B. What is the growth factor for J-Town?
Part C. Use the equation to estimate the population in 2072 to the nearest hundred people.
~~~~~~~~~~~~~~~~~~~
(A) P(t) = 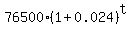 = = 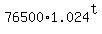 ,
where t are years after 2019 (so 2020 is t= 1, 2021 is t=2 and so on . . . )
(B) the growth factor is 1.024.
(C) P(2072) = ,
where t are years after 2019 (so 2020 is t= 1, 2021 is t=2 and so on . . . )
(B) the growth factor is 1.024.
(C) P(2072) = 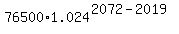 = = 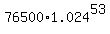 = 268,880.4 (approximately),
and we say that the population will be about 268,900 to the nearest hundred people in 2072. = 268,880.4 (approximately),
and we say that the population will be about 268,900 to the nearest hundred people in 2072.
Solved.
---------------------
To see many other similar and different solved problems on population growth, look into the lesson
- Population growth problems
in this site. The solutions there are given in compact and clear form; to read them is a pleasure.
After reading it, you will be prepared to solve million other similar problems
on population growth on your own, without any help from outside.
Moreover, after reading this lesson you will be able to teach others to this art.
Question 1206097: this year an estimated 4,325,000 people in this country are illiterate. With new incentives and funding, the country is hoping to cut that number by 3% every year. How many people do you predict will be illiterate in the year...
2035
2095
2155
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1205754: what is the inverse of y= 2e^(x-2)
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by ikleyn(52790)   (Show Source): (Show Source):
Question 1205133: 6 divided by y
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1204989: A population numbers 20,000 organisms initially and grows by 1.1% each year.
Suppose P represents population, and t the number of years of growth. An exponential model for the population can be written in the form P = a * b^t where a = ? and b = ?.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
a = 20000 is the starting population
b = 1.011 to represent the 1.1% growth
b = 1+r, where r = 0.011 in this case
If b > 1 then we have exponential growth.
If 0 < b < 1, then there's exponential decay.
Question 1204990: Convert the equation f(t) = 116(0.69)^t to the form f(t) = ae^kt
Find a = ? and k = ?
Round off to three decimal places
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910
|





