Question 1208255: Hi, can you help with this question:
Use x=alphasintheta for sqrt(alpha^2-x^2), x= alphatantheta for sqrt(alpha^2+x^2) and x= alphasectheta for sqrt(x^2-alpha^2), to find int (x/(sqrt(1-x^2)^3) dx
Found 2 solutions by Edwin McCravy, math_tutor2020:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I don't understand the stuff in the beginning, so I skipped on over
to find int (x/(sqrt(1-x^2)^3) dx
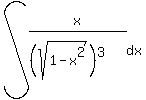
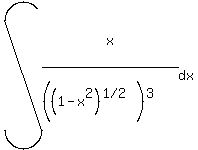
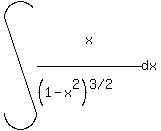
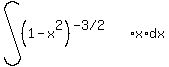 Students nowadays do lots more u substituting than they did in
the old days when I was teaching. We taught "putting in and taking out",
which meant:
"Putting in a factor to cause an expression to become the differential
and offsetting by multiplying on the outside of the integral by its reciprocal."
We would think of, not write, the power rule
Students nowadays do lots more u substituting than they did in
the old days when I was teaching. We taught "putting in and taking out",
which meant:
"Putting in a factor to cause an expression to become the differential
and offsetting by multiplying on the outside of the integral by its reciprocal."
We would think of, not write, the power rule  ,
adding 1 to the exponent and dividing by it.
You need to have an expression for u, a du, and a constant for an exponent.
So for this: ,
adding 1 to the exponent and dividing by it.
You need to have an expression for u, a du, and a constant for an exponent.
So for this:
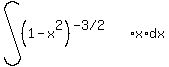 Then we'd think, not write, "u is (1-x2).
Then we'd think, not write, "we need to get a du".
We would observe that the differential of 1-x2 was -2x*dx, and that
we could easily make the x become -2x by multiplying x by -2 and multiplying on
the outside of the integral by the reciprocal of -2 which
is -1/2. That would give us our du. So we'd write this:
Then we'd think, not write, "u is (1-x2).
Then we'd think, not write, "we need to get a du".
We would observe that the differential of 1-x2 was -2x*dx, and that
we could easily make the x become -2x by multiplying x by -2 and multiplying on
the outside of the integral by the reciprocal of -2 which
is -1/2. That would give us our du. So we'd write this:
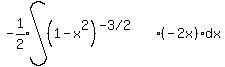 So we'd think, not write, "u is 1-x2 and the (-2x)dx is du,
and then we'd think of the power rule of adding 1 to the exponent and then
dividing by it.
So we'd add 1 to -3/2 and get -1/2
Then we'd divide by the -1/2 and realize that it would cancel with the -1/2
we just put on the outside of the integral (to offset the multiplication by -2) and we'd get
So we'd think, not write, "u is 1-x2 and the (-2x)dx is du,
and then we'd think of the power rule of adding 1 to the exponent and then
dividing by it.
So we'd add 1 to -3/2 and get -1/2
Then we'd divide by the -1/2 and realize that it would cancel with the -1/2
we just put on the outside of the integral (to offset the multiplication by -2) and we'd get
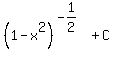 and then and then
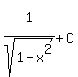 Now if that's too hard for you and you want to do all the substituting that they
are requiring today, go to
https://www.integral-calculator.com/
and they'll go through it step by step for you.
Edwin
Now if that's too hard for you and you want to do all the substituting that they
are requiring today, go to
https://www.integral-calculator.com/
and they'll go through it step by step for you.
Edwin
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
|
|
|