Find the equation of the parabola whose focus is (-3, 2) and directrix is x+y = 4.
By definition a parabola is the set of points each of which is the same
distance from a given point (called the focus) as its perpendicular
distance to a given line (called the directrix).
Let (x,y) be any arbitrary point on the parabola.
The green line is the directrix with equation x+y = 4.
Draw two lines, one from that arbitrary point (x,y)
perpendicular to the directrix and another from (x,y)
to the focus (-3,2):
Those two black lines must be equal in length.
The perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is
d =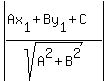 
Therefore the perpendicular distance from any arbitrary point
(x,y) on the desired parabola to the line x+y=4 or x+y-4=0 is
d =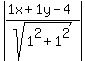 
= 
= 
=
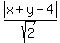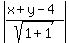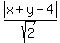The distance between two points (x1,y1) and (x2,y2)
is given by the formula
d = √(x2-x1)²+(y2-y1)²
So the distance from any arbitrary point (x,y) and (-3,2) is given by:
d = √(-3-x)²+(2-y)²
So we set the two distances equal:
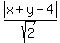= √(-3-x)²+(2-y)²
Multiply both sides by √2
|x+y-4| = √2√(-3-x)²+(2-y)²
Squaring both sides gets rid of the absolute value and the square roots:
(x+y-4)² = 2[(-3-x)²+(2-y)²]
x²+y²+16+2xy-8x-8y = 2[9+6x+x²+4-4y+y²]
x²+y²+16+2xy-8x-8y = 18+12x+2x²+8-8y+2y²
x²+y²+16+2xy-8x-8y = 26+12x+2x²-8y+2y²
-x²+2xy-y²-20x-10 = 0
x²-2xy+y²+20x+10 = 0
Edwin
