 Since both centers are on the red line y = x,
we can let the smaller circle have radius r and center A(r,r)
and let the larger circle have radius R and center B(R,R)
We want to find the difference between between R and r,
so we want to find R-r.
We use the distance formula to find the distance between
the centers A(r,r) and B(R,R)
d =
Since both centers are on the red line y = x,
we can let the smaller circle have radius r and center A(r,r)
and let the larger circle have radius R and center B(R,R)
We want to find the difference between between R and r,
so we want to find R-r.
We use the distance formula to find the distance between
the centers A(r,r) and B(R,R)
d = 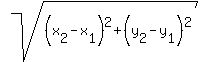 where (x1,y1) = (r,r)
and where (x2,y2) = (R,R)
We are given that the distance between centers is 8.
So we have
where (x1,y1) = (r,r)
and where (x2,y2) = (R,R)
We are given that the distance between centers is 8.
So we have
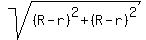 = 8
= 8
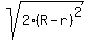 = 8
= 8
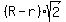 = 8
Divide both sides by
= 8
Divide both sides by  R-r =
R-r = 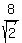 R-r =
R-r = 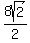 R-r =
R-r =  Edwin
Edwin