Question 694253: find the center and radius of a circle (3x^2)+(2x)+(3y^2)-(7y)-(10)=0 I would like to see the steps as you go along to see how you find the answer. Thank you so much!
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! DISCLAIMER: I do not believe in memorizing multi-step recipes (not my religion), so I will give the logic rationale for a way to solve the problem.
The Pythagorean theorem and the drawing below show why  represents a circle with center (h,k) and radius  . (PREACHING: Memorizing as a formula does not make sense).
We have to find the coordinates of the center (h and k), and the radius r, and with very little extra work, we can get the equation in the form .
From  , you could to get to something that looks like
where (h,k) represents the center of the circle and is the radius.
-->  -->  --> 
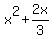 is not a perfect square. To make it into something like
 we would have to add a third term.
(That is called "completing the square", a vocabulary term that often needs to be memorized, to speak the same language as the teachers. I do not object to memorizing a few terms, and I'll allow that one, because it's useful).
For all  ,  , so  gives us the x-coordinate of the center,
and  is the third term we have to add.
The same can be done for 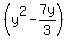 to get it to look like 
 -->  , finding the y-coordinate of the center,
and finding  , the third term we have to add to complete the square.
If we add those third terms to the left side of the equal sign we have to add them to the right side too, so
--> 
Adding the fractions on the right side, and writing the left side as the sum of squares, we get the equation of the circle in the form we want:
-->  -->  --> 
(If we did not care about the equation, all we needed to do is add on the right side).
Now we find the radius  --> 
|
|
|
