 Draw the radius to (6,8). We use the slope
formula to find its slope. It passes through
(x1, y1) = (0,0) and (x2, y2) = (6,8).
m =
Draw the radius to (6,8). We use the slope
formula to find its slope. It passes through
(x1, y1) = (0,0) and (x2, y2) = (6,8).
m =  m =
m = 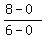 =
=  =
=  = slope of radius to (6,8)
The red line is perpendicular to the radius drawn to to (6,8) because a
tangent is perpendicular to a radius drawn to the point of tangency.
Therefore the slope of the red line is the negative reciprocal of the
slope of the radius to (6,8). So the red line's slope is
= slope of radius to (6,8)
The red line is perpendicular to the radius drawn to to (6,8) because a
tangent is perpendicular to a radius drawn to the point of tangency.
Therefore the slope of the red line is the negative reciprocal of the
slope of the radius to (6,8). So the red line's slope is  .
---
Draw the radius to (8,-6).
.
---
Draw the radius to (8,-6).
 We use the slope
formula to find its slope. It passes through
(x1, y1) = (0,0) and (x2, y2) = (8,-6).
m =
We use the slope
formula to find its slope. It passes through
(x1, y1) = (0,0) and (x2, y2) = (8,-6).
m =  m =
m = 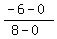 =
= 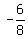 =
=  The green line is perpendicular to the radius drawn to to (8,-6) because a
tangent is perpendicular to a radius drawn to the point of tangency.
Therefore the slope of the green line is the negative reciprocal of the
slope of the radius to (8,-6). So the green line's slope is
The green line is perpendicular to the radius drawn to to (8,-6) because a
tangent is perpendicular to a radius drawn to the point of tangency.
Therefore the slope of the green line is the negative reciprocal of the
slope of the radius to (8,-6). So the green line's slope is  .
The red line is perpendicular to the green line because the red
line's slope is
.
The red line is perpendicular to the green line because the red
line's slope is  and the green line's slope is
and the green line's slope is  and they are negative reciprocals.
Edwin
and they are negative reciprocals.
Edwin