Question 669435: find an equation of a circle that tangent is to 3x+4y-15=0 at (5,0); contains (-2,-1)
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Maybe there is a formula in your book that solves this type of problem.
I do not do types or formulas, so my solution will just stem from the most basic concepts. Sorry if it gets long and boring.
CIRCLE TANGENT TO A LINE:
At the point where a circle is tangent to a line, the radius is perpendicular to that line.
So the center of that circle is on the line perpendicular to  at point (5,0).
<-->  <-->  <-->  ,
so the line has a slope of 
The slope of a line perpendicular to is
 =
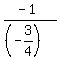The equation of a line with slope that passes through (5,0) is
 <--> 
CIRCLE PASSING THROUGH TWO POINTS:
The center of the circle that passes through (5,0) and (-2,-1) is at the same distance from those two points,
so it is on the perpendicular bisector of the segment joining those two points.
The perpendicular bisector is perpendicular to that segment and passes through the midpoint of that segment.
The midpoint of that segment, calculated from the coordinates of (5,0) and (-2,-1) is
( , )=( , )
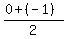The slope of that segment, calculated from the coordinates of (5,0) and (-2,-1) is
and the slope of a perpendicular line is  =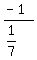
The equation of the line with slope passing through (,) is
 <-->  <-->  <-->  <--> 
THE CENTER OF OUR CIRCLE:
The center of the circle we are looking for is on the lines
 and  .
Those lines are not parallel, so they intersect at one point.
That point is the center of the circle.
We need to solve 
 -->  (multiplying both sides times 3)
-->  -->  -->  -->  -->  --> 
Substituting  into ,
 -->  --> 
So the center of the circle is (2,-4).
THE RADIUS OF THE CIRCLE:
The radius  is the distance from circle center (2,-4) to circle point (5,0).
We can calculate 
THE EQUATION OF THE CIRCLE"
The equation of a circle centered at (2,-4) and with  is
 --> 
|
|
|
