Question 664492: I have the Lat Lon coordinates of three points that lie on a large circle (radius somewhere between 12-15 miles). How can I find the Lat Lon of the center of the circle? The differences in elevation are less than 100', so I assume one can assume flat earth.
I'm not even certain as to how to try this, as I've been out of school over 40 years and most things of this sort that I learned are pretty well gone at this point.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! DISCLAMER:
I have not seen a solution to this type of problem before, so my ideas on how to solve it (described below) may not be the best way to do it.
Maybe the navy uses an easy program for that type of calculation.
FIRST CONDSIDERATIONS:
The size of that circle is small enough that a flat map would be an accurate representation of the curved, hilly earth surface with those 3 points.
If you have such a map, with a convenient scale, you could graphically find the center of the circle. (That would entail drawing line segments connecting the points, and constructing their perpendicular bisectors)
If you cannot do geometrical constructions on a map, or don't trust the accuracy of that method, you would have to use algebra calculations.
Unless, you are close to one of the poles, the latitude and longitude lines could be considered a set ot x-y coordinates, and you could use algebra/analytical geometry to calculate the coordinates of the centter of your circle.
THE CONCEPT:
Three points form a triangle. From the geometry point of view, each side is a line segment.
For each side of the triangle, the points that are at the same distance of both ends are located on the perpendicular bisector of that segment. The perpendicular bisector is a line perpendiculat to the segment, passing through the midpoint of the segment.
If you draw the perpendicular bisectors for all three sides of the triangle, they will all meet at one point.
That point will be at the same distance from all 3 vertices of the triangle.
That point will be the center of the circle the 3 points (vertices of the triangle) are on. (It is called the circumcenter of the triangle).
You only need any 2 of the 3 perpendicular bisectors to locate that point.
Searching for perpendicular bisector, and circumcenter you would be able to find many drawings, videos, interactive stuff, and explanations. Some of those will help you more than whatever I can draw and descibe here.
GEOMETRICAL CONSTRUCTIONS ON A MAP:
The perpendicular bisector of a segment connecting point A to point B can be constructed on a map with a compass and straightedge.
(A ruler can be considered a straightedge).
You set the compass to have a fixed distance between the pointy end and the marking end.
(Making that distance just a bit longer than the segment AB will work well).
Placing the pointy end of the compass on one end of the segment (let's say point A), you trace arcs to one side of the segment and the other, aiming to cover a point where you expect the perpendicular bisector to pass.
You do the same from the other end of the segment (point B).
The arcs drawn from both ends will meet, at points on either side of your segment.
Connecting theose points will give you the perpendicular bisector.
For a segment between points A and B, the construction would look like this:
 I drew the "arcs" in red, and the bisector line in green. I drew the "arcs" in red, and the bisector line in green.
(My "arcs" are really straight lines, because I could not draw them curved, as they should be).
USING ALGEBRA /ANALYTIC GEOMETRY (works if you are not close to the poles):
We give the coordinates for each point as a pair ( , , ), ),
for example, (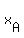 , ,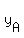 ) for point A, where ) for point A, where
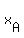 = latitude of point A = latitude of point A
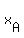 = longitude of point A. = longitude of point A.
We could set up equations for the perpendicular bisector lines for segments AB and BC,
and find where they intersect.
We could also set up equations stating that the three points are at the same distance from the center of the circle.
I could try to write a formula for the coordinates of the center, but it is going to be complicated.
I an not sure I can do it without typos, and I am not sure you would find it useful.
There are formulas available in some websites (for example in the "circumscribed circle" entry in Wikipedia).
THE EASIER "CHEAT":
There are also web calculators (websites that will calculate for you if you enter the coordinates of your three points). Search the web for "coordinates of circumcenter calculator".
That last option could be your best bet.
|
|
|