Question 482339: Consider the Venn diagram below. The numbers in the regions of the circle indicate the number of items that belong to that region. Since the diagram wont copy, the left circle "A" contains a "20", the right circle "B" contains a "50" and the center, shared space contains a "70".
Determine
n(A)
n(B)
P(A)
P(B)
P(A|B)
P(B|A)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your venn diagram should look like this.
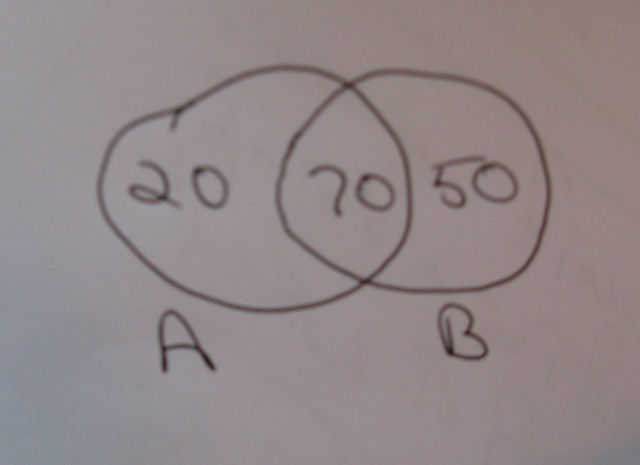
Answers to your questions are shown below:
n(A) = the number of elements in A.
That would be 20 + 70 = 90.
20 are in A only.
70 are in both A and B.
n(B) = the number of elements in B.
That would be 50 + 70 = 120.
50 are in B only.
70 are in both B and A.
P(A) = probability of an element shown being in set A.
There are 20 + 70 + 50 = 140 elements in the universe shown.
That universe is A union B.
A union B is the set of all elements that are either in A, or in B, or in both.
Since there are 90 elements in A and there are 140 elements overall, the probability of an element being in set A would be 90 / 140.
P(B) = probability of an element shown being in set B.
There are 20 + 70 + 50 elements in the universe shown.
That universe is A union B.
A union B is the set of all elements that are either in A, or in B, or in both.
Since there are 120 elements in B and there are 140 elements overall, the probability of an element being in set B would be 120 / 140.
P(A|B) = the probability of an element being in A given that it is in B.
Since B contains 120 elements, and the elements that are also in A are 70, then the probability of an element being in A given that it is in B would be 70 / 120.
P(B|A) = the probability of an element being in B given that it is in A.
Since A contains 90 elements, and the elements that are also in B are 70, then the probability of an element being in B given that it is in A would be 70 / 90.
Note that the formula for the number of elements in A union B is the elements in A plus the elements in B minus the elements that are in both A and B.
The number of elements in A is equal to 90.
The number of elements in B is equal to 120.
The number of elements in A intersect B is equal to 70.
The number of elements in A union B are therefore 90 + 120 - 70 = 140.
Your Venn Diagram already shows that relationship.
The number 20 on the left are the elements that are in A only.
The number 50 on the right are the elements that are in B only.
The 70 in the middle are the elements that are in both A and B.
Add them up and you get 140 total elements.
The number of elements in A are 20 + 70.
The number of elements in B are 50 + 70.
You can see the 70 are being double counted because they are the same 70 shown in the middle of the Venn Diagram.
|
|
|