SOLUTION: (55) Equilateral triangle ABC, with a side of length 4, is inscribed in a circle. The midpoint of AB is D and the midpoint of AC is E. If DE is extended to meet the circle at F, fi

Point F is obtained by extending DE to intersection with the circle.

Extend DE in the opposite direction to intersection with the circle in point G.

Then, due to symmetry, EF = DG. 


Let x be the length of EF.


Now we have two intersecting chords GF and AC, and we are going to apply the theorem 
about intersecting chords.


The intersection point E divides chord AC in two equal intervals, AE = EC = 4/2 = 2 units long, each.

The intersection point E divides chord GF in two intervals, EF = x and GE = 2+x units long.


Now apply the theorem about intersecting chords

    AE * EC = GE * EF,

or

    2*2 = (2+x)*x.


Simplify and find x from this equation

    4 = 2x + x^2,

    x^2 + 2x - 4 = 0,

     =  =  =  = .


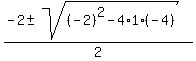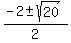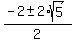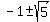We reject the negative root and keep the positive root.


Thus we get the 

ANSWER.  The length of EF is   = 1.2361 units  (approximately).