SOLUTION: Derive the equation of the locus of a point P(x,y) which moves so that its distance from (2,3) is always equal to its distance from the line x+2=0

Algebra ->  Circles -> SOLUTION: Derive the equation of the locus of a point P(x,y) which moves so that its distance from (2,3) is always equal to its distance from the line x+2=0      Log On


   

Question 1191710: Derive the equation of the locus of a point P(x,y) which moves so that its distance from (2,3) is always equal to its distance from the line x+2=0
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
Use the definition of Parabola. Your given focus is (2,3), and directrix is x=-2.


( Notice that the vertex is (0,3) in case you choose to use one of the parabola formulas directly.)
-----

The points equally distant from (2,3) and from x=-2

%28x-2%29%5E2%2B%28y-3%29%5E2=%28x-%28-2%29%29%5E2%2B%28y-y%29%5E2
- - -
%28x-2%29%5E2%2B%28y-3%29%5E2=%28x%2B2%29%5E2%2B0
%28x-2%29%5E2-%28x%2B2%29%5E2=-%28y-3%29%5E2
x%5E2-4x%2B4-%28x%5E2%2B4x%2B4%29=-%28y-3%29%5E2
-8x=-%28y-3%29%5E2
highlight%288x=%28y-3%29%5E2%29---------notice here, the vertex is shown from the equation as (0,3).

Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
Derive the equation of the locus of a point P(x,y) which moves so that
its distance from (2,3) is always equal to its distance from the line x+2=0.
~~~~~~~~~~~~~~~~ 

The line x+2 = 0 is the line  x= -2  (vertical line parallel to y-axis with x-coordinate of -2).


Let (x,y) be the point of the locus.  Then the distance from (x,y) to the line x= -2 is  |x+2|
(notice the absolute value sign).


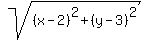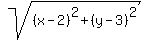The distance from (x,y) to the point (2,3)  is  sqrt%28%28x-2%29%5E2+%2B+%28y-3%29%5E2%29.


The equation of the locus is

   sqrt%28%28x-2%29%5E2+%2B+%28y-3%29%5E2%29 = |x+2|.



Square both sides and get

    (x-2)^2 + (y-3)^2 = (x+2)^2

    x^2 - 4x + 4 + y^2 - 6y + 9 = x^2 + 4x + 4

    y^2 - 6y + 9 = 8x

    (y-3)^2 = 8x


It is final equation of the locus.  It represents a parabola with the horizontal axis y= 3, 
parallel to x-axis. The parabola is opened right. Its vertex is the point (x,y) = (0,3).

Solved.



Answer by greenestamps(13198) About Me  (Show Source):
You can put this solution on YOUR website!


You don't need to use the "equal distance" information to write and simplify an equation that says the distance from the point is equal to the distance from the line.

The given information defines a parabola with directrix x=-2 and focus (2,3).

With directrix x=-2 and focus (2,3), the vertex is (0,3). The parabola opens to the right; the equation in vertex form is

x-h=%281%2F%284p%29%29%28y-k%29%5E2%29

where (h,k) is the vertex and p is the directed distance (i.e., could be negative) from the vertex to the focus.

In this problem, (h,k) is (0,3) and p is 2. So the equation is

x-0=%281%2F8%29%28y-3%29%5E2

or

x=%281%2F8%29%28y-3%29%5E2

or

8x=%28y-3%29%5E2