SOLUTION: A square is inscribed in a circle. If the area of the square is 9 in squared, what is the ratio of the circumference of the circle to the area of the circle?

Algebra ->  Circles -> SOLUTION: A square is inscribed in a circle. If the area of the square is 9 in squared, what is the ratio of the circumference of the circle to the area of the circle?       Log On


   

Question 1065051: A square is inscribed in a circle. If the area of the square is 9 in squared, what is the ratio of the circumference of the circle to the area of the circle?
Found 2 solutions by ikleyn, KMST:
Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.
A square is inscribed in a circle. If the area of the square is 9 in squared, what is the ratio of the circumference of
the circle to the area of the circle?
~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

The ratio of the the circumference of the circle to the area of the circle is

%282%2Api%2Ar%29%2F%28pi%2Ar%5E2%29 = 2%2Fr.


We are given a%5E2 = 9.


Hence, a = 3.


Therefore,  r = %28a%2F2%29%2Asqrt%282%29 = 1.5%2Asqrt%282%29.


Then the ratio of the circumference of the circle to the area of the circle is 2%2F%281.5%2Asqrt%282%29%29 = sqrt%282%29%2F1.5 = %282%2Asqrt%282%29%29%2F3 1%2Fin.


Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
NOTE: This is a strange problem wording,
and I suspected a typo in the wording you posted.
If so, check the wording carefully and post again.

For a square ,
area=side%5E2 <---> side=sqrt%28area%29 .
In this case, for the square in the problem,
side=sqrt%289in%5E2%29=3in .
With the square inscribed in a circle ,
the diameter, 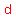red%28d%29 , of the circle
is the diagonal, 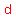red%28d%29 , of the square.
According to the Pythagorean theorem,
red%28d%29%5E2=red%283in%29%5E2%2Bred%283in%29%5E2=2%2A9in%5E2 ,
so
d=sqrt%282%2A9in%5E2%29=sqrt%282%29%2Asqrt%289%29in=3sqrt%282%29in .
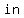For any circle, radius=diameter%2F2 ,
area=pi%2Aradius%5E2 , and
circumference=pi*diameter=pi*radius/2}}} .
For any circle,
the ratio of circumference of the circle to the area of the circle is
%28pi%2Aradius%2F2%29%2F%28pi%2Aradius%5E2%29=2%2Fradius .
For the circle in the problem,
radius=3sqrt%282%29%2F2in ,
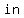and we could calculate that ratio as
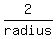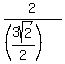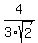2%2Fradius%22=%222%2F%28%283sqrt%282%29%2F2%29%29%22=%224%2F3sqrt%282%29%22=%222sqrt%282%29%2F3 ,
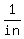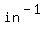with units of 1%2Fin or in%5E%28-1%29 .
Maybe you were expected to calculate
circumference=3sqrt%282%29%2Apiin ,
radius=3sqrt%282%29%2F2in ,
area=pi%2A%283sqrt%282%29%2F2%29%5E2in%5E2=pi%2A9%2A2%2F4in%5E2=9pi%2F2in%5E2 ,
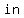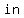and then further calculate the ratio as
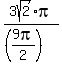3sqrt%282%29%2Api%2F%28%289pi%2F2%29%29%22=%222sqrt%282%29%2F3 ,
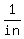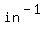with units of 1%2Fin or in%5E%28-1%29 .