Question 1043513: The centre of a circle passing through the points(0,0) , (1,0) and touching the circle x^2+y^2=9
Found 2 solutions by ikleyn, KMST:
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The center of a circle passing through the points (0,0), (1,0) and touching the circle x^2+y^2=9
~~~~~~~~~~~~~~~~~~~~~~~~~~~
 = 9 (1)
is the circle of the radius 3 with the center at (0,0), the origin of the coordinate system.
The other circle passes through the point (0,0), so these two circles can not have external touching.
Hence, they have internal touching.
The center of the smaller circle lies in the straight line x = 0.5 (vertical line which bisects the segment [(0,0) - (1,0)].
Then the radius of the smaller circle is = 9 (1)
is the circle of the radius 3 with the center at (0,0), the origin of the coordinate system.
The other circle passes through the point (0,0), so these two circles can not have external touching.
Hence, they have internal touching.
The center of the smaller circle lies in the straight line x = 0.5 (vertical line which bisects the segment [(0,0) - (1,0)].
Then the radius of the smaller circle is 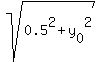 with an unknown with an unknown  .
From the other side, since the smaller circle touches the large circle internally, the center of the smaller circle lies
on the circle of the radius .
From the other side, since the smaller circle touches the large circle internally, the center of the smaller circle lies
on the circle of the radius  with the center at the origin.
Thus the center of the smaller circle lies in the intersection of the straight line x = 0.5 and the circle of the radius with the center at the origin.
Thus the center of the smaller circle lies in the intersection of the straight line x = 0.5 and the circle of the radius
 with the center at the origin. So, to find with the center at the origin. So, to find  , we have to solve the system of equations , we have to solve the system of equations
 = = 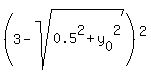 , (1) , (1)
 = = 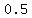 , (2) , (2)
 = =  , (3)
Great !! Now, substitute (2) and (3) into (1). You will have , (3)
Great !! Now, substitute (2) and (3) into (1). You will have
 = = 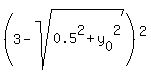 . (4)
Thus you have a single equation (4) for . (4)
Thus you have a single equation (4) for  to solve.
Equation (4) is equivalent to to solve.
Equation (4) is equivalent to
 = = 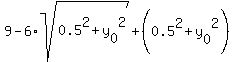 , or , or  = = 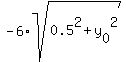 , or , or 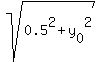 = =  = =  .
Square both side of the last equation. You will get .
Square both side of the last equation. You will get
 = =  ---> --->  = = 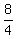 = 2 ---> = 2 --->  = +/- = +/- .
Answer. Thus we found two and only two points that there are the centers.
One point is ( .
Answer. Thus we found two and only two points that there are the centers.
One point is (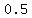 , , ) and the other is ( ) and the other is (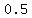 , , ). ).
Solved.
By the way, you have this free of charge online textbook on Geometry
GEOMETRY - YOUR ONLINE TEXTBOOK
in this site.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Since the new circle you are looking for passes through  and and  , ,
those two points are equidistant from the center  of the new circle, of the new circle,
and that means that center is on the bisectrix of segment  . .
That bisectrix is the line  , with equation , with equation  . .
If the new circle touches (meaning it is tangent to the circle  with radius with radius  , ,
then the radii of the two circles at the point of tangency  are on the same line are on the same line  . .
So,  is a radius of circle is a radius of circle  , ,
and a diameter of the new circle,
and  , ,
meaning that  . .
Applying the Pythagorean theorem to right triangle  , we have , we have

 . .
OF course, there are two possibilities:
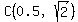 as in the drawing above, with the new circle mostly above the x-axis, or as in the drawing above, with the new circle mostly above the x-axis, or
 if the new circle "hangs mostly below the x-axis." if the new circle "hangs mostly below the x-axis."
|
|
|