SOLUTION: There are two circles, C of radius 1 and Cr of radius r, which intersect on a plane. At each of the two intersecting points on the circumferences of C and Cr, the tangent to C a

We only need to draw the tangents at one of the points of
intersections of C and Cr. For the tangents at the other
point of intersection will be essentially the same.

As we have it drawn here, the smaller circle is C and the larger
circle is Cr.

Here's how we draw the above figure, step by step.

1. We draw a circle with center O and radius 1.
2. We draw a tangent line AB
3. We draw a radius OT which is perpendicular to 
tangent line AB.
4. We draw PQ through T so that ∠PTB = 120°
It will be tangent to the other circle we will draw.
5. We draw UV through T perpendicular to PQ.
6. We choose an arbitrary point C on UV between 
U and T to be the center of the second circle, so
that the 120° ∠PTB will be outside both circles.
7. We draw the second circle with center C and radius 
CT.
8. We label CT as r the radius of the second circle.
9. We draw CO and label it d, the distance between
the two centers.

Now we must show that ∠CTO = 60°.

Here is why.

∠PTB = 120° by construction.
∠PTA = 60° because it is supplementary to ∠PTB.
∠PTC = 90° by construction.
∠ATC = 30° by subtracting ∠PTA from right ∠PTC
∠ATO = 90° by construction
∠CTO = 60° by subtracting ∠ATC from right ∠ATO

Now we can use the law of cosines on ΔCOT

CO² = CT²+OT²-2∙CT∙OT∙cos(∠CTO)

d² = r²+1²-2∙r∙1∙cos(60°)
d² = r²+1-2∙r∙1/2
d² = r²+1-r
d² = r²-r+1


That's the part (1), writing d in terms of r.

d will be a minimum if and only if d² is a minimum.

Let d² = y

Then

y = r²-r+1

That's a quadratic so we can use the vertex formula
to find the x-coordinate of the vertex

-b/(2a) = -(-1)/(2∙1) = 1/2.

[or if you are taking calculus, you can get that by the
methods of calculus like this  y' = 2r-1=0, so r=1/2)]

So the minimum value of y is attained when r =1/2.
Substituting,

y = (1/2)²-(1/2)+1
y = 1/4-1/2+1
y = 1/4-2/4+4/4
y = 3/4

Therefore the minimum value of d² is 3/4,
and so the minimum value of d is .

Note that the arbitrary point C we picked above on UV
in part (1) was not at all where d was a minimum.  
But that was OK because we weren't trying to get
d as a minimum in (1), we were just getting an
equation for d in terms of r.

The second circle Cr would have been much smaller, not
larger, than circle C.  Here's how it would look if we 
had picked the point C that would have made d a minimum.



Notice that the triangle COT is now a 
30°-60°-90° right triangle.

So we use the second figure, cut down a bit.



We want to find the area of the overlapping region of the
two circles. We drew in the radius OS.

The lower part of the overlapping region is one/half of the
area of the smaller circle.  Its radius is 1/2.
The area of the WHOLE small circle is  or
, so the area of the
semicircle which is the lower part of the overlapping
region is .

Now we get the upper half of the overlapping region.
That is the circle segment (small D-shaped region bounded 
by ST and the small arc which ST subtends.)

To find the area of that small circle segment, we find 
the area of the sector SOT (shaped like a piece of pie)
and then find the area of equilateral ΔSOT and
subtract it from the area of the sector.

The area of a sector is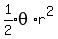 
where theta is in radians. Since ΔSOT is equilateral,
∠SOT = 60° =  radians.  So the area of sector SOT
is .

We must subtract the area of equilateral ΔSOT from that.
The area of ΔSOT is . ST=1 and CO=
So the area of ΔSOT is 
So the area of the small circle segment just above ST is


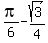So we add the area of the lower half the small circle to the
small segment and get






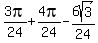
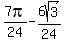
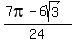Edwin