Question 1019885: Obtain the equations of the circles which touch the y axis and pass through the points (2,5) and (4,3)
Found 2 solutions by Edwin McCravy, solver91311:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If a circle touches the y-axis, then its radius equals
the x-coordinate of the center. That is, r=h. The center (h,k)
becomes (r,k).
 So the equation is of the form:
So the equation is of the form:
 The points (2,5) and (4,3) must satisfy this equation, so we have
this system of equations to solve:
The points (2,5) and (4,3) must satisfy this equation, so we have
this system of equations to solve:
 Working with the first equation:
Working with the first equation:



 Working with the second equation:
Working with the second equation:



 We can eliminate r by multiplying the results
of the first equation by -2 and adding to
the results of the second equation:
We can eliminate r by multiplying the results
of the first equation by -2 and adding to
the results of the second equation:







 k=3, k=11
Substituting k=3 in
k=3, k=11
Substituting k=3 in





 So the small circle has
center (2,3) and radius 2, and it has
equation
So the small circle has
center (2,3) and radius 2, and it has
equation

 Substituting k=11 in
Substituting k=11 in





 So the large circle has
center (10,11) and radius 10, and it has
equation
So the large circle has
center (10,11) and radius 10, and it has
equation

 Edwin
Edwin
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since the points ) and and ) are on the desired circles, segment are on the desired circles, segment  is a chord. Using the two-point form of a linear equation, the derived slope-intercept form of the line passing through the two given points is is a chord. Using the two-point form of a linear equation, the derived slope-intercept form of the line passing through the two given points is  . .
Since the center of a circle lies on the perpendicular bisector of any chord of a circle and the mid-point of segment AB is the point ) , the equation of the perpendicular bisector of the chord, and hence the relationship between the coordinates of either of the center points of the two desired circles is: , the equation of the perpendicular bisector of the chord, and hence the relationship between the coordinates of either of the center points of the two desired circles is:

Since the desired circles are tangent to the  -axis, the centers must lie on lines parallel to the -axis, the centers must lie on lines parallel to the  -axis through the point of tangency. Referring to the diagram, the two centers are -axis through the point of tangency. Referring to the diagram, the two centers are ) and and ) , and the centers must lie on the lines , and the centers must lie on the lines  and and  or or  . Also, the points of tangency are . Also, the points of tangency are ) and and )
.jpg)
Note that segments  , ,  , and , and  are all radii of the desired circles and must perforce be of equal measure. Same thing for segments are all radii of the desired circles and must perforce be of equal measure. Same thing for segments  , ,  , and , and  . .
Using the distance formula without being specific about which of the centers we use gives us:
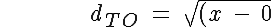^2\ +\ (y\ -\ y)^2}\ =\ x)
and
^2\ +\ (y\ -\ 5)^2})
but we will find it convenient to use the relationship  to substitute to substitute  for for  in this distance formula. in this distance formula.
^2\ +\ (x\ -\ 4)^2})
Since the two radii must be of equal measure:
^2\ +\ (x\ -\ 4)^2}\ =\ x)
Square both sides, expand the squared binomials, and collect terms gives us:

which factors to
(x\ -\ 10)\ =\ 0)
Hence

and

And if  then then  , hence , hence  . Whereas if . Whereas if  then then  , hence , hence  . .
The standard form equation of a circle of radius  centered at centered at ) is is ^2\ +\ (y\ -\ k)^2\ =\ r^2) . .
Hence, your two equations are:
^2\ +\ (y\ -\ 3)^2\ =\ 4)
and
^2\ +\ (y\ -\ 11)^2\ =\ 100)
John

My calculator said it, I believe it, that settles it

|
|
|