SOLUTION: Find the interior angles of the triangle with the given vertices (1,2) (3,4) (2,5)

You can do this two different ways.

Method 1:
A. Use the distance formula to find the length of the three sides.
B. Use then law of cosines.

Method 2:
1. Find the slopes of the three sides.
2. Use the tangent formula for the angles between two sides.

Method 2 is easier.

Let's draw the triangle and extend the sides:

(1,2) (3,4) (2,5)




We  use the slope formula, which is

m = 

three times to find these three slopes:

the slope of the green line is m = 1
the slope of the red line is m = 3
the slope of the blue line is m = -1

Here is the formula for the acute angle between two lines, one with
slope m1  and the other with slope m2.



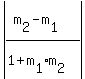with each pair of lines.  Except when two lines are perpendicular
there are TWO angles between any pair of lines, an acute angle and an
obtuse angle which are supplementary.      

If the denominator of that fraction
comes out 0, making it undefined, that means the angle between
the two lines are perpendicular and the angle between them is 90°.

I'll just find the angle between the green and red lines. You find
the others:






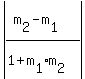
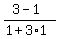
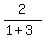
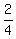Using the inverse tangent function on a calculator, we get

q = 26.56505118°.

That's the acute angle between the green and red lines.
The obtuse angle between them is 180°-26.56505118° or 153.4349488°

The acute angle between the red and blue lines is 63.43494882°
The obtuse angle between them is 180°-63.43494882° or 116.5650512°.

The angle between the green and blue line is 90°.  (You can also
tell that because their slopes are negative reciprocals 1 and -1.)

Since it is a right triangle the other two angles besides the
right angle are acute angles.

Answers: 26.56505118°, 63.43494882°, 90° 

Edwin