|
Question 1195990: A car moving in a straight line passes through two points A and B, which are 120m apart, with speeds 72m/s and 56m/s respectively. Calculate the (i) retardation of the car (ii) distance beyond the second point B at which the car wil come to rest (iii) time taken to cover the distance in (ii) above
Answer by ikleyn(52812)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A car moving in a straight line passes through two points A and B, which are 120m apart,
with speeds 72m/s and 56m/s respectively. Calculate the
(a)  deceleration of the car deceleration of the car
(b) distance beyond the second point B at which the car wil come to rest
(c) time taken to cover the distance in (b) above
~~~~~~~~~~~~~~~~~~
"Retardation" is not a professional term to use in this situation.
The professional term is "deceleration", which I used, when edited your post.
(a) Let "m" be the mass of the car, and let "a" be the deceleration.
Write the mechanic energy conservation law
maS = 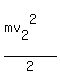 - - 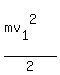 . (1)
Here " ma " is the deceleration force (by the Newton's second law);
" S " is the distance between the points;
" maS " is the mechanical work performed by the force "ma"; . (1)
Here " ma " is the deceleration force (by the Newton's second law);
" S " is the distance between the points;
" maS " is the mechanical work performed by the force "ma";
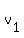 and and 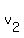 are velocities of the car at given points.
Formula (1) says that the change of kinetic energy (right side) is equal to
the work done by the force ma on the distance S (left side).
Cancel "m" in both sides of the equation (1) and substitute given values. You will get
a*120 = are velocities of the car at given points.
Formula (1) says that the change of kinetic energy (right side) is equal to
the work done by the force ma on the distance S (left side).
Cancel "m" in both sides of the equation (1) and substitute given values. You will get
a*120 =  - -  56^2/2 - 72^2/2
120a = -1024
a = -1024/120 = -8.533 (rounded).
Thus deceleration is 8.533 m/s^2. It is the ANSWER for part (a).
The sign " minus, - " means deceleration as opposite to acceleration. 56^2/2 - 72^2/2
120a = -1024
a = -1024/120 = -8.533 (rounded).
Thus deceleration is 8.533 m/s^2. It is the ANSWER for part (a).
The sign " minus, - " means deceleration as opposite to acceleration.
Part (a) is solved.
(b) To solve (b), use the same formula (1), but this time in different form
maS = - (2) (because the speed at the stop condition is zero now)
This formula (2) expresses the same as formula (1) above.
Cancel "m" in both sides of the equation (2) and substitute given values. You will get
-8.533*S = - (2) (because the speed at the stop condition is zero now)
This formula (2) expresses the same as formula (1) above.
Cancel "m" in both sides of the equation (2) and substitute given values. You will get
-8.533*S = - 8.533*S = 1568
S = 1568/8.533 = 183.76 (rounded)
Thus the deceleration distance to get full stop is 183.76 meters.
It is the ANSWER to part (b).
8.533*S = 1568
S = 1568/8.533 = 183.76 (rounded)
Thus the deceleration distance to get full stop is 183.76 meters.
It is the ANSWER to part (b).
Part (b) is solved.
(c) To find time "t" to stop after passing point B, use the formula
S = 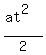 .
Substitute S = 183.76 m and a = 8.533 here and get
t = .
Substitute S = 183.76 m and a = 8.533 here and get
t =  = =  = 6.563 seconds.
It is the ANSWER to part (c). = 6.563 seconds.
It is the ANSWER to part (c).
Solved.
-------------------
To see another similar problem, solved earlier at this forum, look at this link
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1183954.html
https://www.algebra.com/algebra/homework/Permutations/Permutations.faq.question.1183954.html
|
|
|
| |