SOLUTION: Please help me solve this question - Find the perimeter of the figure whose vertices are The midpoints of a quadrilateral with vertices at (7,4) (1,8) (-3,4) and (3,-2)

Click here to see ALL problems on Points-lines-and-rays

Question 1100667: Please help me solve this question - Find the perimeter of the figure whose vertices are The midpoints of a quadrilateral with vertices at (7,4) (1,8) (-3,4) and (3,-2)

Found 3 solutions by richwmiller, greenestamps, ikleyn:
Answer by richwmiller(17219)   (Show Source):
You can put this solution on YOUR website!
First step : find the midpoints of the 4 sides.
(7,4) (1,8)

Solved by pluggable solver: Midpoint

The first point is (x1,y1). The second point is (x2,y2)

Since the first point is (7, 4), we can say (x1, y1) = (7, 4)
So ,

Since the second point is (1, 8), we can also say (x2, y2) = (1, 8)
So ,

Put this all together to get: , , , and

----------------------------------------------------------------------------------------

Finding the x coordinate of the midpoint: Add up the corresponding x coordinates x1 and x2 and divide that sum by 2

X Coordinate of Midpoint =

X Coordinate of Midpoint =

X Coordinate of Midpoint =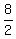

X Coordinate of Midpoint =

So the x coordinate of the midpoint is 4

----------------------------------------------------------------------------------------

Finding the y coordinate of the midpoint: Add up the corresponding y coordinates y1 and y2 and divide that sum by 2

Y Coordinate of Midpoint =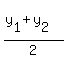

Y Coordinate of Midpoint =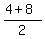

Y Coordinate of Midpoint =

Y Coordinate of Midpoint =

So the y coordinate of the midpoint is 6

===============================================================================

Summary:

The midpoint of the segment joining the two points (7, 4) and (1, 8) is (4, 6).

So the answer is (4, 6)

(1,8) (-3,4)

Solved by pluggable solver: Midpoint

The first point is (x1,y1). The second point is (x2,y2)

Since the first point is (1, 8), we can say (x1, y1) = (1, 8)
So ,

Since the second point is (-3, 4), we can also say (x2, y2) = (-3, 4)
So ,

Put this all together to get: , , , and

----------------------------------------------------------------------------------------

Finding the x coordinate of the midpoint: Add up the corresponding x coordinates x1 and x2 and divide that sum by 2

X Coordinate of Midpoint =

X Coordinate of Midpoint =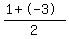

X Coordinate of Midpoint =

X Coordinate of Midpoint =

So the x coordinate of the midpoint is -1

----------------------------------------------------------------------------------------

Finding the y coordinate of the midpoint: Add up the corresponding y coordinates y1 and y2 and divide that sum by 2

Y Coordinate of Midpoint =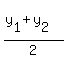

Y Coordinate of Midpoint =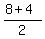

Y Coordinate of Midpoint =

Y Coordinate of Midpoint =

So the y coordinate of the midpoint is 6

===============================================================================

Summary:

The midpoint of the segment joining the two points (1, 8) and (-3, 4) is (-1, 6).

So the answer is (-1, 6)

(-3,4)(3,-2)

Solved by pluggable solver: Midpoint

The first point is (x1,y1). The second point is (x2,y2)

Since the first point is (-3, 4), we can say (x1, y1) = (-3, 4)
So ,

Since the second point is (3, -2), we can also say (x2, y2) = (3, -2)
So ,

Put this all together to get: , , , and

----------------------------------------------------------------------------------------

Finding the x coordinate of the midpoint: Add up the corresponding x coordinates x1 and x2 and divide that sum by 2

X Coordinate of Midpoint =

X Coordinate of Midpoint =

X Coordinate of Midpoint =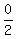

X Coordinate of Midpoint =

So the x coordinate of the midpoint is 0

----------------------------------------------------------------------------------------

Finding the y coordinate of the midpoint: Add up the corresponding y coordinates y1 and y2 and divide that sum by 2

Y Coordinate of Midpoint =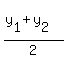

Y Coordinate of Midpoint =

Y Coordinate of Midpoint =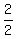

Y Coordinate of Midpoint =

So the y coordinate of the midpoint is 1

===============================================================================

Summary:

The midpoint of the segment joining the two points (-3, 4) and (3, -2) is (0, 1).

So the answer is (0, 1)

(3,-2)(7,4)

Solved by pluggable solver: Midpoint

The first point is (x1,y1). The second point is (x2,y2)

Since the first point is (3, -2), we can say (x1, y1) = (3, -2)
So ,

Since the second point is (7, 4), we can also say (x2, y2) = (7, 4)
So ,

Put this all together to get: , , , and

----------------------------------------------------------------------------------------

Finding the x coordinate of the midpoint: Add up the corresponding x coordinates x1 and x2 and divide that sum by 2

X Coordinate of Midpoint =

X Coordinate of Midpoint =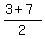

X Coordinate of Midpoint =

X Coordinate of Midpoint =

So the x coordinate of the midpoint is 5

----------------------------------------------------------------------------------------

Finding the y coordinate of the midpoint: Add up the corresponding y coordinates y1 and y2 and divide that sum by 2

Y Coordinate of Midpoint =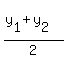

Y Coordinate of Midpoint =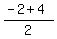

Y Coordinate of Midpoint =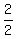

Y Coordinate of Midpoint =

So the y coordinate of the midpoint is 1

===============================================================================

Summary:

The midpoint of the segment joining the two points (3, -2) and (7, 4) is (5, 1).

So the answer is (5, 1)

(4, 6)
(-1, 6)
(0, 1)
(5, 1)
Second step: find the distances from midpoint to midpoint
1st distance (4, 6)(-1, 6)

Solved by pluggable solver: Distance Formula

The first point is (x1,y1). The second point is (x2,y2)

Since the first point is (4, 6), we can say (x1, y1) = (4, 6)
So ,

Since the second point is (-1, 6), we can also say (x2, y2) = (-1, 6)
So ,

Put this all together to get: , , , and

--------------------------------------------------------------------------------------------

Now use the distance formula to find the distance between the two points (4, 6) and (-1, 6)

Plug in , , , and

==========================================================

Answer:

The distance between the two points (4, 6) and (-1, 6) is exactly 5 units

2nd (-1, 6)(0, 1)

Solved by pluggable solver: Distance Formula

The first point is (x1,y1). The second point is (x2,y2)

Since the first point is (-1, 6), we can say (x1, y1) = (-1, 6)
So ,

Since the second point is (0, 1), we can also say (x2, y2) = (0, 1)
So ,

Put this all together to get: , , , and

--------------------------------------------------------------------------------------------

Now use the distance formula to find the distance between the two points (-1, 6) and (0, 1)

Plug in , , , and

==========================================================

Answer:

The distance between the two points (-1, 6) and (0, 1) is exactly units

The approximate distance between the two points is about 5.09901951359278 units

So again,

Exact Distance: units

Approximate Distance: units

3rd (0, 1)(5, 1)

Solved by pluggable solver: Distance Formula

The first point is (x1,y1). The second point is (x2,y2)

Since the first point is (0, 1), we can say (x1, y1) = (0, 1)
So ,

Since the second point is (5, 1), we can also say (x2, y2) = (5, 1)
So ,

Put this all together to get: , , , and

--------------------------------------------------------------------------------------------

Now use the distance formula to find the distance between the two points (0, 1) and (5, 1)

Plug in , , , and

==========================================================

Answer:

The distance between the two points (0, 1) and (5, 1) is exactly 5 units

4th (5, 1)(4, 6)

Solved by pluggable solver: Distance Formula

The first point is (x1,y1). The second point is (x2,y2)

Since the first point is (5, 1), we can say (x1, y1) = (5, 1)
So ,

Since the second point is (4, 6), we can also say (x2, y2) = (4, 6)
So ,

Put this all together to get: , , , and

--------------------------------------------------------------------------------------------

Now use the distance formula to find the distance between the two points (5, 1) and (4, 6)

Plug in , , , and

==========================================================

Answer:

The distance between the two points (5, 1) and (4, 6) is exactly units

The approximate distance between the two points is about 5.09901951359278 units

So again,

Exact Distance: units

Approximate Distance: units

Third step:add up the four distances
I'll leave that for you.
And the lesson to learn from this solution is THIS:
It is beneficial to learn many methods.
NEVER depend on any one method used by little ikleyn when you want to solve any problem!
She thinks she has the only solution and only her method is worth considering.
Get over yourself, little girl.
One of the many wonders of math is that there are many approaches to problems. Each one teaches something different. Each student can decide which approach suits them. It is beneficial to learn many methods.

Answer by greenestamps(13209)   (Show Source):
You can put this solution on YOUR website!

Unfortunately, the other tutor had an incorrect input for finding the 4th midpoint....

The four midpoints are
-1,6
4,6
0,1
5,1 (not 5,3)

For two of the sides of the resulting quadrilateral, you don't need the distance formula, because the sides are horizontal line segments; the lengths of those two segments are just the differences between the x coordinates. That will mean less work required to get the final answer.

Other than that, proceed as shown by the other tutor.

Answer by ikleyn(52878)   (Show Source):
You can put this solution on YOUR website!
.
It is VERY WELL KNOWN FACT that "the figure whose vertices are the midpoints of a quadrilateral" is a parallelogram,
and the sides of this figure are the mid-segments of triangles diagonals cut the given quadrilateral.

See the lesson
    - Midpoints of a quadrilateral are vertices of the parallelogram
in this site.

Therefore, to calculate the perimeter of the "figure" and answer the problem's question, all you need to do
is to find the lengths of two diagonals of the GIVEN quadrilateral and then add them.

It can be done in three lines:

1) The length of the diagonal from (7,4) to (-3,4) is = = 10 (! notice this diagonal is vertical segment !). 2) The length of the diagonal from (1,8) to (3,-2) is = = = = . 3) the sum of the diagonals' lengths is = 20.198 (approximately), and it is the perimeter of the "figure" under the question.

This problem is not about calculations.

It is to check whether you know Geometry.

And the lesson to learn from this solution IS THIS:

NEVER follow the approach used by @richwmiller when solve problems like this !