|
Question 1058774: Given two segments with lengths a and b, construct a segment with length sqrt(ab).
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Given two segments with lengths a and b, construct a segment with length sqrt(ab).
~~~~~~~~~~~~~~~~~~~~~~
The construction algorithm is as follows.
1. Using the straightedge and compass, construct in the straight line a segment AD of the length "a" and adjacent
to it a segment DB of the length "b", with the common endpoint and starting point D.
2. Using the straightedge and compass, bisect the segment AB and find its central point (midpoint) O.
3. Using the compass, draw the semicircle with the center at the point O of the radius equal to the half of the length
of the segment AB (so, the radius of the semi-circle is the segment OA = OB).
4. Using the straightedge and compass,, erect/construct the perpendicular to the straight line at the point D of merging AD and BD.
Draw/proceed the perpendicular till the intersection with the semi-circle. Let C be the intersection point
of the perpendicular and semi-circle.
5. The segment DC is what you need: its length is 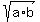 , the geometric mean of "a" and "b".
See the lesson
- Arithmetic mean and geometric mean inequality - Geometric interpretations
in this site, where this construction algorithm is described and illustrated.
See the lesson
- HOW TO bisect a segment using a compass and a ruler
where the basic construction procedures are described.
You have this free of charge online textbook on Geometry
- GEOMETRY - YOUR ONLINE TEXTBOOK
in this site.
The last referred lesson is the part of this textbook under the topic "Geometric constructions using a compass and a ruler. Basic operations".
|
|
|
| |
