|
Tutors Answer Your Questions about Points-lines-and-rays (FREE)
Question 1186939: Suppose that O=(0,0), A=(3.4,0), and B=(2.81,1.92). The arc between points B and C is 12.92 units long.
A. What is the value of (theta)1, the radian measure of Angle AOB?
B. What is the value of (theta)2, the radian measure of Angle BOC?
C. What are the x- and y-coordinates of point C?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Strictly saying, this problem is posed INCORRECTLY,
since it does not define that point 'C' lies in the same circle as points 'A' and 'B'.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the solution, broken down step by step:
**A. θ₁ (Angle AOB):**
1. **Find the lengths of OA and OB:**
* OA = √((3.4 - 0)² + (0 - 0)²) = 3.4
* OB = √((2.81 - 0)² + (1.92 - 0)²) = √(7.8961 + 3.6864) = √11.5825 ≈ 3.403
2. **Use the dot product formula:**
* OA • OB = |OA| * |OB| * cos(θ₁)
* (3.4 * 2.81) + (0 * 1.92) = 3.4 * 3.403 * cos(θ₁)
* 9.554 = 11.5702 * cos(θ₁)
* cos(θ₁) = 9.554 / 11.5702 ≈ 0.8257
3. **Solve for θ₁:**
* θ₁ = arccos(0.8257) ≈ 0.5994 radians
**B. θ₂ (Angle BOC):**
1. **Find the radius of the circle:** Since OA and OB are radii, and we are working with a circular arc BC, OA is the radius. r = 3.4
2. **Use the arc length formula:**
* Arc length (s) = r * θ₂
* 12.92 = 3.4 * θ₂
* θ₂ = 12.92 / 3.4 ≈ 3.8 radians
**C. Coordinates of Point C:**
1. **Find the angle from the x-axis to OC:** This is θ₁ + θ₂ ≈ 0.5994 + 3.8 = 4.3994 radians.
2. **Use the coordinates formula:**
* x = r * cos(θ₁ + θ₂) = 3.4 * cos(4.3994) ≈ -1.0468
* y = r * sin(θ₁ + θ₂) = 3.4 * sin(4.3994) ≈ -3.2348
**Therefore:**
* θ₁ (Angle AOB) ≈ 0.5994 radians
* θ₂ (Angle BOC) ≈ 3.8 radians
* Coordinates of point C ≈ (-1.0468, -3.2348)
Question 1166974: P is the centre of a circle that passes through O, and O is the centre of a circle that passes through P. If angle C=66 degrees, then the measure of angle OPB, in degrees is:
A) 120
B) 125
C) 116
D) 128
E) 124
https://imageshack.com/i/pnM6OEIVj
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1180852: TV weather forecasters use satellite and radar data to predict where storms will move in order to help viewers know what weather to expect. The map below shows a storm off the eastern coast of the United States. The arrows show the path the heart of the storm traveled over the last 48 hours. If you were a forecaster in the northeast, use the map to answer the following questions.
https://api.agilixbuzz.com/Resz/~0.6NT8GFszQyEepNgJ.U8Pc_1Jw6w7bKhdBO1lgK6sThuzD160XdxwpKkVzzWg/48780464,FA7,11,3/Assets/Media/Images/41.2-HOT3-Weather.jpg
a. What would you tell your Northeast coast audience? Which type of reasoning—inductive or deductive—did you use? Explain.
b. Write an if-then statement to describe your conjecture.
c. Write the inverse of the statement.
d. Write the converse and contrapositive of the statement.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's an analysis of the storm's path and how a forecaster might present the information:
**a. What to tell the Northeast coast audience:**
"Good evening, everyone. As you can see on the map, a storm is currently located off the East Coast. Over the past 48 hours, it has followed a generally westward track, as indicated by these arrows. Based on this observed pattern, we can *induce* that the storm is likely to continue moving in a westerly direction. This means it *could* potentially impact the Northeast coast in the coming days. However, it's important to note that storm tracks can change, so we'll continue to monitor the situation closely and provide updates as they become available. We urge everyone in coastal areas to stay informed and prepare for possible severe weather."
* **Type of reasoning:** Inductive reasoning was used. Inductive reasoning involves making generalizations based on observed patterns or specific instances. The forecaster observed the storm's past track and *induced* that it would likely continue on a similar path. It's important to emphasize the uncertainty inherent in inductive reasoning ("could," "possibly") as the observed pattern doesn't *guarantee* future behavior.
**b. If-then statement (Conjecture):**
If a storm has moved westward for the past 48 hours, then it will continue to move westward.
**c. Inverse of the statement:**
If a storm has *not* moved westward for the past 48 hours, then it will *not* continue to move westward.
**d. Converse and Contrapositive:**
* **Converse:** If a storm continues to move westward, then it has moved westward for the past 48 hours.
* **Contrapositive:** If a storm does *not* continue to move westward, then it has *not* moved westward for the past 48 hours.
Question 1209705: Find the slope of the line
y
=
3
2
x
+ 2
.
Simplify your answer and write it as a proper fraction, improper fraction, or integer.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll provide a similar example.
Let's say the example equation is  , in which you can write as y = (7/5)x+39 , in which you can write as y = (7/5)x+39
Compare that to y = mx+b
m = 7/5 = slope
b = 39 = y intercept
Use that example to determine the slope of y = (3/2)x+2
Question 1188287: Given triangle ABC with D the midpoint of side AB and E on side BC, F on side AC and G is the intersection of side DE and side BF. BE:EC = 2:3 and DG:GE = 5:8. What is the ratio of BG:GF?
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! Certainly, let's find the ratio of BG:GF.
**1. Utilize Ceva's Theorem:**
* Ceva's Theorem states that for any triangle ABC, if lines AD, BE, and CF intersect at a single point (in this case, point G), then:
(AF/FC) * (BD/DA) * (CE/EB) = 1
**2. Apply the given ratios:**
* BD/DA = 1/1 (since D is the midpoint of AB)
* BE/EC = 2/3
**3. Calculate AF/FC:**
* Using Ceva's Theorem:
(AF/FC) * (1/1) * (3/2) = 1
AF/FC = 2/3
**4. Use Menelaus' Theorem:**
* Menelaus' Theorem states that for any transversal line (in this case, line DE) that intersects the sides of a triangle (triangle ABC) at points D, E, and F, then:
(AD/DB) * (BE/EC) * (CF/FA) = 1
**5. Apply the known ratios and solve for BG/GF:**
* (1/1) * (2/3) * (3/2) * (BG/GF) = 1
BG/GF = 1
**Therefore, the ratio of BG:GF is 1:1.**
Let me know if you have any other questions or problems to solve!
Question 1195764:
Let’s assume the following statements are true: Historically, 75% of the five-star football recruits in the nation go to universities in the three most competitive athletic conferences. Historically, five-star recruits get full football scholarships 93% of the time, regardless of which conference they go to. If this pattern holds true for this year’s recruiting class, answer the following:
a. Based on these numbers, what is the probability that a randomly selected five-star recruit who chooses one of the best three conferences will be offered a full football scholarship?
b. What are the odds a randomly selected five-star recruit will not select a university from one of the three best conferences? Explain.
c. Explain whether these are independent or dependent events. Are they Inclusive or exclusive? Explain.
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Probability of a full scholarship for a recruit in a top conference:**
* Given:
* 75% of five-star recruits go to top three conferences.
* 93% of five-star recruits get full scholarships.
* Since the probability of getting a full scholarship is independent of the conference chosen (given in the problem), the probability of a five-star recruit in a top three conference getting a full scholarship is simply **93%**.
**b) Odds of a recruit NOT selecting a top three conference:**
* Probability of selecting a top three conference: 75%
* Probability of NOT selecting a top three conference: 100% - 75% = 25%
* Odds are typically expressed as a ratio of the probability of an event occurring to the probability of the event not occurring.
* Odds against selecting a top three conference:
* (Probability of NOT selecting) / (Probability of selecting)
* = 25% / 75%
* = 1/3
* Therefore, the odds of a randomly selected five-star recruit NOT selecting a university from one of the three best conferences are **1 to 3**.
**c) Independence and Inclusivity/Exclusivity:**
* **Independence:**
* The probability of a recruit getting a full scholarship is independent of the conference they choose. This is stated in the problem.
* **Inclusivity/Exclusivity:**
* The events "selecting a top three conference" and "not selecting a top three conference" are **mutually exclusive**. This means a recruit cannot simultaneously select a top three conference and not select a top three conference.
**In Summary:**
* a) Probability of a full scholarship for a recruit in a top conference: 93%
* b) Odds of a recruit NOT selecting a top three conference: 1 to 3
* c) Scholarship probability and conference choice are independent events.
* Selecting a top three conference and not selecting a top three conference are mutually exclusive events.
Question 1208981: One square is placed upon another so that a regular octagon is formed, along with eight right isosceles triangles each with its hypotenuse on a side of the octagon. If the perimeter of the octagon is 18 cm, find the perimeter of the star, in cm.
https://ibb.co/3MVhbWy
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a TWIN problem was solved at this forum many years ago under this link
https://www.algebra.com/algebra/homework/Length-and-distance/Length-and-distance.faq.question.1148864.html
Question 1208847: P(-2,1) y=1/4x-3
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You didn't state what you want. Do you want the equation of the line through
P(-2,1) parallel (or maybe perpendicular) to the line y=1/4x-3?
Do you want the distance from the point P(-2,1) to the line y=1/4x-3?
You must tell us what you want us to do. Otherwise, we can't know.
Edwin
Question 1207455: ABC is a triangle with ∠CAB=15
∘
and ∠ABC=30
∘
. If M is the midpoint of AB, Sin then ∠ACM= ?
Found 3 solutions by ikleyn, Edwin McCravy, greenestamps:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
ABC is a triangle with ∠CAB=15∘ and ∠ABC=30∘.
If M is the midpoint of AB, find ∠ACM.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution by Edwin is perfect and deserves admiration.
My congratulations to Edwin with this great achievement.
I came to bring a shorter solution.
The given part is shown in Figure 1 below.
 Figure 1.
Triangle ABC has the angles A= 15°, B= 30° and C= 180°-15°-30°= 135°.
We want to find angle
Figure 1.
Triangle ABC has the angles A= 15°, B= 30° and C= 180°-15°-30°= 135°.
We want to find angle  .
Draw perpendicular CH from vertex C to the base AB (Figure 2). .
Draw perpendicular CH from vertex C to the base AB (Figure 2).
 Figure 2.
First part of the solution is the same as that of Edwin' solution,
and it shows that a =
Figure 2.
First part of the solution is the same as that of Edwin' solution,
and it shows that a =  , b = , b =  .
The rest of the solution is different (very simple and totally geometrical).
Triangle BHC is a right-angled triangle with the acute angle B of 30°.
Hence, the opposite leg CH is half of the hypotenuse BC
CH = .
The rest of the solution is different (very simple and totally geometrical).
Triangle BHC is a right-angled triangle with the acute angle B of 30°.
Hence, the opposite leg CH is half of the hypotenuse BC
CH =  = = 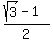 , (1)
while its other leg BH is , (1)
while its other leg BH is  times the hypotenuse BC
BH = times the hypotenuse BC
BH = 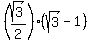 = = 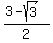 .
Then the segment MH is the complement of BH to 1
MH = 1 - .
Then the segment MH is the complement of BH to 1
MH = 1 - 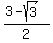 = =  = = 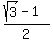 . (2)
Comparing expressions (1) and (2), we see that CH = MH.
Hence, right-angled triangle MHC is isosceles right-angled triangle,
which implies that angle MCH is 45°.
Thus ∠ACM = 135° - 60° - 45° = 30°,
and the problem is solved completely. . (2)
Comparing expressions (1) and (2), we see that CH = MH.
Hence, right-angled triangle MHC is isosceles right-angled triangle,
which implies that angle MCH is 45°.
Thus ∠ACM = 135° - 60° - 45° = 30°,
and the problem is solved completely.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1206891: Indicate in standard form the equation of the line passing through the given points, writing the answer in the equation box below.
G (4, 6), H (1, 5)
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Indicate in standard form the equation of the line passing through the given points,
writing the answer in the equation box below.
G (4, 6), H (1, 5)
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @josgarithmetic is WRONG.
It is incorrect from the first step calculating the slope and to the end, including his answer  . .
I came to bring a correct solution.
Calculate the slope m =  = = 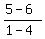 = = 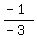 = =  .
It is the same as to use the formula m = .
It is the same as to use the formula m =  with coordinates with coordinates  = 4, = 4,  = 6, = 6,  = 1, = 1,  = 5.
Next, write an equation of the line having the slope = 5.
Next, write an equation of the line having the slope  and passing through the given point (4,6).
An equation of a straight line in a coordinate plane which has the slope m and passes through the given point P = (a,b) is
y - b = m*(x-a).
Substitute here m = and passing through the given point (4,6).
An equation of a straight line in a coordinate plane which has the slope m and passes through the given point P = (a,b) is
y - b = m*(x-a).
Substitute here m =  , a = 4, b = 6, and you will get
y - 6 = , a = 4, b = 6, and you will get
y - 6 = 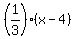 . (1)
It is the equation in the slope-point form.
But you want to get an equation in standard form, which is Ax + By = C.
To get it, multiply equation (1) by 3 (both sides) and simplify
3*(y-6) = x-4,
-18 + 4 = x - 3y,
-14 = x - 3y,
x - 3y = -14.
This equation is what you want, i.e. your ANSWER. . (1)
It is the equation in the slope-point form.
But you want to get an equation in standard form, which is Ax + By = C.
To get it, multiply equation (1) by 3 (both sides) and simplify
3*(y-6) = x-4,
-18 + 4 = x - 3y,
-14 = x - 3y,
x - 3y = -14.
This equation is what you want, i.e. your ANSWER.
----------------
See the lesson
- Equation for a straight line in a coordinate plane passing through two given points
in this site. Find there several other similar solved problems.
Learn the subject from there.
As a bonus to you, consider the lessons in this site
- Find the slope of a straight line in a coordinate plane passing through two given points
- Equation for a straight line having a given slope and passing through a given point
- Solving problems related to the slope of a straight line
- Equation for a straight line in a coordinate plane passing through two given points
- Equation for a straight line parallel to a given line and passing through a given point
- Equation for a straight line perpendicular to a given line and passing through a given point
that are closely related to your problem.
Consider them as your textbook, handbook, tutorials and (free of charge) home teacher.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1206892: Indicate in standard form the equation of the line passing through the given points, writing the answer in the equation box below.
E ( - 2, 2), F (5, 1)
Found 3 solutions by josgarithmetic, Theo, MathLover1:
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the points are (-2,2), (5,1)
let x1,y1 = -2,2 and x2,y2 = 5,1
slope = (y2-y1)/(x2-x1) = (1-2)/(5+2) = -1/7
use one of the points to get the y-intercept.
general slope intercept form equation is y = mx + b
m is the slope
b is the y-intercept
when the slope is -1/7, equation becomes y = -1/7 * x + b
use (5,1) coordinate and replace y with 1 and x with 5 to get:
1 = -1/7 * 5 + b
solve for b to get:
b = 1 + 5/7 = 12/7
equation becomes y = -1/7 * x + 12/7.
that's the slope intercept form of the equation.
to get the standard form, do the following:
add -1/7 * x to both sides of the equation to get 1/7 * x + y = 12/7
multiply both sides of the equation by 7 to get x + 7y = 12
that's the standard form of the equation.
here's the graph.

note that the standard form and the slope intercept form of the equation draw the same line.
that's because they're equivalent.
the two speciied points are on the line.
they are (-2,2) and (5,1)
the slope intercept is (0,1.714) where 1.714 represents the fraction 12/7.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
| Solved by pluggable solver: Finding the Equation of a Line |
First lets find the slope through the points ( , , ) and ( ) and ( , , ) )
 Start with the slope formula (note: ( Start with the slope formula (note: ( , , ) is the first point ( ) is the first point ( , , ) and ( ) and ( , , ) is the second point ( ) is the second point ( , , )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator  to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 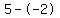 to get to get 
So the slope is

------------------------------------------------
Now let's use the point-slope formula to find the equation of the line:
------Point-Slope Formula------
 where where  is the slope, and ( is the slope, and ( , , ) is one of the given points ) is one of the given points
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite 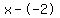 as as 
 Distribute Distribute 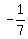
 Multiply Multiply 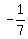 and and  to get to get 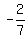
 Add Add  to both sides to isolate y to both sides to isolate y
 Combine like terms Combine like terms 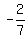 and and  to get to get  (note: if you need help with combining fractions, check out this solver) (note: if you need help with combining fractions, check out this solver)
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line which goes through the points ( , , ) and ( ) and ( , , ) is: ) is:
The equation is now in  form (which is slope-intercept form) where the slope is form (which is slope-intercept form) where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the points ( and plot the points ( , , ) and ( ) and ( , , ), we get this: (note: if you need help with graphing, check out this solver) ), we get this: (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , , ) )
Notice how the two points lie on the line. This graphically verifies our answer.
|
 ....write in standard form ....write in standard form  , both sides multiply by , both sides multiply by 


Question 1064005: ΔABC has vertices at A(5,2), B(−3,1), and C(−2,5). Point D is located on the intersection of the altitude and AB�, in such a way that D has coordinates at approximately (−1.52,1.18).
https://cds.flipswitch.com/tools/asset/media/607812
Match each question with the correct measurement, rounded to one decimal place.
What is the approximate area of the triangle?
What is the approximate length of the base of the triangle for the given altitude?
What is the approximate length of the altitude of the triangle?
16.1 units
3.9 units
8.1 units
7.6 units
15.8 units
8.0 units
Found 5 solutions by math_tutor2020, MathTherapy, greenestamps, ikleyn, mananth:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers:
Area = 15.8 square units
Base = 8.1 units
Altitude = 3.9 units
--------------------------------------------------------------------------
Explanation
Use the distance formula to determine the length of side AB
A = (x1,y1) = (5,2) and B = (x2,y2) = (-3,1)






 approximately approximately

Follow similar steps to find the distance from C = (-2,5) to D = (-1.52,1.18) is roughly 3.85004 which rounds to 3.9
Then,
area of triangle = 0.5*base*height
area = 0.5*AB*CD
area = 0.5*8.1*3.9
area = 15.795
area = 15.8 square units.
There's rounding error going on here.
The area of triangle ABC should be 15.5 square units exactly.
This can be determined in the next section below.
--------------------------------------------------------------------------
When given the coordinates of the vertex points, we could use the shoelace formula to fairly quickly find the area of any polygon.
Given list of vertex points
(5,2)
(-3,1)
(-2,5)
Make a copy of the first point (5,2) and place it at the bottom of the list
(5,2)
(-3,1)
(-2,5)
(5,2)
This will help form a loop.
Space the x and y coordinates out. Each (x,y) point gets its own row.

Then draw in the diagonals as indicated below.

Multiply along the red diagonal pairs and add up those products.
5*1+(-3*5)+(-2*2) = 5-15-4 = -14
Do the same for the blue diagonal pairs.
5*5+(-2*1)+(-3*2) = 25-2-6 = 17
Subtract the results.
red - blue = -14 - 17 = -31
We get a negative result. Let's take the absolute value to get |-31| = 31
Lastly, take half of this to get the area = (1/2)*31 = 15.5
The area of the triangle is exactly 15.5 square units.
GeoGebra can be used to verify.
More practice on the shoelace formula is found here
--------------------------------------------------------------------------
What's another way to see how the area is exactly 15.5?
My post is already quite lengthy so this section will be a brief overview rather than getting into the gritty details.
The distance formula will show that
AB = sqrt(65)
The equation of line AB is y = (1/8)x + 11/8
The equation of line CD is y = -8x - 11
Intersect those two equations to determine point D is at the exact location (-99/65, 77/65)
Note how -99/65 = -1.52 and 77/65 = 1.18 approximately.
So that's where your teacher is getting (-1.52, 1.18) for point D.
Use the distance formula to determine that CD = 31/sqrt(65)
Then lastly,
area = 0.5*base*height
area = 0.5*AB*CD
area = 0.5*sqrt(65)*( 31/sqrt(65) )
area = 0.5*31
area = 15.5
which is exact without any rounding done to it.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
ΔABC has vertices at A(5,2), B(−3,1), and C(−2,5). Point D is located on the intersection of the altitude and AB�, in such a way that D has coordinates at approximately (−1.52,1.18).
https://cds.flipswitch.com/tools/asset/media/607812
Match each question with the correct measurement, rounded to one decimal place.
What is the approximate area of the triangle?
What is the approximate length of the base of the triangle for the given altitude?
What is the approximate length of the altitude of the triangle?
16.1 units
3.9 units
8.1 units
7.6 units
15.8 units
8.0 units
The EASIEST and BEST method to determine the AREA of any POLYGON is the SHOELACE METHOD!
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Interesting problem; and interesting responses....
Finding the area of the triangle using the coordinates of A, B, C, and D in the formula for the area of a triangle (one-half base times height) is not a particularly good way. For one thing the coordinates of D are only given approximately; for another thing, you end up doing ugly arithmetic with decimal approximations of the lengths of the base and height.
On the other hand, since the problem asks to find lengths rounded to the nearest tenth, you can get the answer that way.
But, wait -- using either that approximate method or any of at least two exact methods, the correct answer of (exactly) 15.5 is not one of the answer choices. So here the problem is faulty....
Finally, as a note regarding the response from the other tutor, you should never take it as the gospel truth when someone says that a particular method is the best way to work a problem. Enclosing the triangle in a rectangle and finding the area of the given triangle as the area of the rectangle minus the area of the three small triangles is A good way to solve the problem; but there are other equally good ways.
The length of the base AB is found simply using the Pythagorean Theorem -- although again, given the set of answer choices and the instruction to find the length to the nearest tenth, 8.1 is the obvious answer.
And, finally, only one of the answer choices is reasonable for the length of altitude AD.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Here I will explain you how to find quickly the area of triangle ABC
with the vertices at the integer grid points in a coordinate plane.
Draw the minimal rectangle on the grid which concludes the given triangle.
Identify the triangles on the grid inside this rectangle that are outside the given triangle.
It is quite easy to find the area of each such a triangle.
After that, you will find the area of your triangle ABC mentally, by subtraction
the areas of the three other triangles from the area of rectangle.
Notice that doing this way, You will find the PRECISE area of triangle ABC mentally and quickly,
without doing boring calculations.
It is the best strategy and the most valuable piece of knowledge, which you can learn from this problem.
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find AB by distance formula
A(5,2) B(-3,1)
AB = sqrt((2-1)^2+(5-(-3))^2) =sqrt(65) Base of triangle
C=(-2,5) , D(-1.52,1.18)
CD = sqrt((-2+1.52)^2+(5-(1.18))^2) =3.85
Area of triangle = 1/2 *8.06*3.85
15.5 unit^2
Question 1206482: Given the two circles defined by the equations x^(2)-6x+y^(2)+8y=12 and x^(2)+y^(2)=4y, find the algebraic equation of the line connecting their centers.
Found 3 solutions by greenestamps, math_tutor2020, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If you need to find the centers and radii of the two circles, then you need to complete the squares.
In this problem, you are to find the equation of the line connecting the centers of the circles. That means you don't need to know the radii of the two circles; and that means completing the square is unnecessary work.
As tutor @ikleyn says, you can find the centers of the two circles mentally:
First circle: (x^2-6x+...)+(y^2+8y+...) = ... ---> center (3,-4)
Second circle: (x^2)+(y^2-4y+...) = ... ---> center (0,2)
Then finding the equation of the line containing those two centers is a basic algebraic process.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given the two circles defined by the equations x^(2)-6x+y^(2)+8y=12 and x^(2)+y^(2)=4y,
find the algebraic equation of the line connecting their centers.
~~~~~~~~~~~~~~~~~~~
To find the centers, apply completing the squares separately to x-terms and y-terms in each equation.
It can be done MENTALLY.
The center of the 1st circle is the point (3,-4).
The center of the 2nd circle is the point (0,2).
The slope of the line through the centers is m = 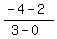 = = 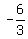 = -2.
So, an equation of the line can be presented in the form
y-2 = m*(x-0),
or
y - 2 = -2x, or y = -2x + 2,
or in any other equivalent form.
You can check on your own that the presented equations are satisfied with
the coordinates of the centers, so this straight line goes through these points. = -2.
So, an equation of the line can be presented in the form
y-2 = m*(x-0),
or
y - 2 = -2x, or y = -2x + 2,
or in any other equivalent form.
You can check on your own that the presented equations are satisfied with
the coordinates of the centers, so this straight line goes through these points.
Solved.
Question 1206483: A bug lives on a corner of a cube and is allowed to travel only on the edges of the cube. In how many ways can the bug visit each of the other seven corners once and only once, returning to its home corner only at the end of the trip?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
See the solution 2 under this link
https://artofproblemsolving.com/wiki/index.php/2006_AMC_12A_Problems/Problem_20
They say that if you are able to understand it, then you are officially good in Math.
Question 1074065: The segment AB is one third of the entire length of segment AD. If A(3,-2) and B(0,2), then where is the terminal point D located?
Found 3 solutions by ikleyn, greenestamps, mananth:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The segment AB is one third of the entire length of segment AD.
If A(3,-2) and B(0,2), then where is the terminal point D located?
~~~~~~~~~~~~~~~~~~~~~
By the way, segment AD may have an OPPOSIITE direction comparing with AB,
or any other direction on the plane, different from that of AB, so this problem,
as it is worded in the post, is HEAVILY DEFECTIVE.
From the written post, it remains unclear how the point B does relate to the segment AD.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Of course, we don't HAVE to use the formula shown by the other tutor. If you want to solve the problem using formal mathematics, there are alternative forms of the formula that make it easier to understand.
But solving the problem informally using common sense is MUCH easier.
B is one-third of the distance from A to D.
In the x direction, from A to B is a change of -3, so from A to D the change in the x direction is 3(-3) = -9. So the x coordinate of D is 3+(-9) = -6.
In the y direction, from A to B is a change of +4, so from A to D the change in the y direction is 3(+4) = +12. So the y coordinate of D is (-2)+12 = 10.
ANSWER: D(-6,10)
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! We have to use section formula for internal division
if we have a point P(x,y) that divides the line segment with marked points as A (x1,y1) and B(x2,y2). To find the coordinates, we use the section formula, which is mathematically expressed as:
P(x, y) = (mx2+nx1)/(m+n), (my2+ny1)/(m+n)
 . .
A= (x2,y2)~(3,-2)
B= (x,y) ~(0,2)
m=1 , n=2
0= (1(x)+(2)(3))/3
x=-6
2= ((1)(y)+(2)(-2))/3
6= y-4
y=10
x(-6,10)
Question 1115219: T(-10,-2) R(10,8) Y(11,-9) are vertices of ∆TRY
1) find equation of YA, the altitude from Y to TR . show that A(4,5)
2) if equation of perpendicular bisector is y=3x-7, find equation of circle through T, R, Y .
3) find the area of ∆TRY
4) find size of angle T
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Equation of TR
x1 y1 x2 y2
-10 -2 10 8
slope m = (y2-y1)/(x2-x1)
( 8 - -2 )/( 10 - -10
( 10 / 20 )
m= 0.50
Plug value of the slope and point ( -10 , -2 ) in
Y = m x + b
-2.00 = -5 + b
b= -2.00 - -5
b= 3
So the equation of TR will be
Y = 1/2 x + 3 ( m=1/2)..................................(1)
AY is perpendicular to TR y=(11,-9)
slope of AY = -2 ( negative reciprocal)
Equation AY
slope =2 , Y=(11,-9)
(y-(-9))= (-2)(x-11)
y+9= -2x+22
y= -2x+13.................................................(2)
Solve (1)&(2) to get point A (4,5)
 . .
--------------------
Question 1206377: A machinist in a fabrication shop needs to bend a metal rod at an angle of 60° at a point 4m from one end of the rod so that the ends of the rod are 12m apart.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! This suggests to use Law Of Cosines to find some value t, the distance from the bend point
to the other end point of the rod.
Draw the figure described in your problem description.
One end point given as 4 meters from one end point and t is distance from bend point to the
other end point of the rod.

Solve for t.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A machinist in a fabrication shop needs to bend a metal rod at an angle of 60°
at a point 4m from one end of the rod so that the ends of the rod are 12m apart.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Do you have a question ?
Question 1205759: Determine if the angle is complementary, supplementary, or vertical. Find the value of x in the figure.
angle AB = (x+8)
angle BC = 2x
What is the value of x?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
The diagram is missing. Also it's a bit strange how your teacher named each angle using two letters. Normally 3 letters are involved.
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1205320: Question Number 11 of 20 - Geometry
Circle O with radius 10.
The area of the shaded sector of circle O
is -
f 50π
g 25π
h 5π
j 20π
Found 2 solutions by MathLover1, josgarithmetic:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! You need to do better than this!
At least you can find (easily) that the whole circle's area is 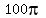 . Whatever else your description is missing, if you look at it (on your end where you are), the answer should be obvious. . Whatever else your description is missing, if you look at it (on your end where you are), the answer should be obvious.
Question 1204896: The segment joining (-2,-3), (6,1) is extended each way a distance equal to one-fourth its own length. Find the terminal points.
Found 2 solutions by math_tutor2020, mananth:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
A = (-2, -3)
B = (6, 1)
The horizontal gap from A to B is 8 units.
Use a number line to see there are 8 spaces between -2 and 6.
Or subtract and use absolute value:  or or 
Absolute value is needed since a negative distance isn't valid.
One quarter of this 8 unit horizontal gap is 8/4 = 2 units.
Let p = 2
The vertical gap from A to B is 4 units.
One quarter of which is 4/4 = 1.
Let q = 1.
When starting at A(-2,-3), move p = 2 units left and q = 1 unit down.
This has us arrive at C(-4,-4) as shown in the tutor @mananth's diagram
Now focus on point B(6,1)
We move p = 2 units right and q = 1 unit up to arrive at D(8,2).
Refer to that same diagram.
In summary, segment AB extends out to CD such that
A = (-2, -3)
B = (6, 1)
C = (-4,-4)
D = (8,2)
GeoGebra is a very useful tool to confirm the answers.
Side notes:
AB = 4*AC
AB = 4*BD
CD = (3/2)*AB
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! The segment joining (-2,-3), (6,1) is extended each way a distance equal to one-fourth its own length. Find the terminal points.
The distance between A(-2,-3),B (6,1) is
AB = 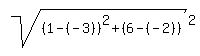 =24 =24
Let C(x1,y1) be the point extended on side of A by 6 units. (1/4)*24=6
Section formula for internal division
P=(((mx2+nx1)/(m+n)),((my2+ny1)/(m+n)))
m and n is the ratio of division
B divides AD in the ratio of 4:1
6=4*x2+1*(-2))/ (4+1)
x1=8
-1= (1*(-3))+4(y1)/(4+1)
y1=2
D(8,2)
In Segment ABC A divides CB in the ratio of 1:4
-2=( (4*x1+1*(6))/(4+1)
solve
x1=-4
-3= (4)*(y2)+(1)(1)))/(4+1)=-4
y1=-4
C(-4,-4)
 . .
Question 1203782: 𝐸 is the midpoint of 𝐷F. 𝐷𝐸 = 4𝑥 + 3
and 𝐸𝐹 = 8𝑥 − 9. Find 𝐷𝐸, 𝐸𝐹, and 𝐷�
Found 2 solutions by MathLover1, mananth:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
𝐸 is the midpoint of 𝐷F. 𝐷𝐸 = 4𝑥 + 3
and 𝐸𝐹 = 8𝑥 − 9. Find 𝐷𝐸, 𝐸𝐹, and 𝐷
Since e is the midpoint of DF DE = EF
Therefore 4x+3 = 8x-9
subtract 8x from both sides of equation
4x+3-8x = -9
substract 3 from both sides
4x -8x = -9-3
-4x = -12
x = -12/-4=3
DE = 4x+3
plug x
DE = 4*3+3
DE = 15
Therefore EF = 15
Question 1203609: Consider two circles, a smaller one and a larger one. If the larger one has a radius that is 16 feet larger than that of smaller circle and the ratio of the circumferences is 15:1, what are the radii of the two circles?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
x = smaller radius
x+16 = larger radius
C = 2*pi*r = circumference formula
C = 2*pi*x = circumference of smaller circle
C = 2*pi*(x+16) = circumference of larger circle
The two circle perimeters are in ratio 15:1
larger/smaller = 15/1
2*pi*(x+16)/(2*pi*x) = 15/1
(x+16)/x = 15/1
1*(x+16) = 15*x
x+16 = 15x
15x-x = 16
14x = 16
x = 16/14
x = 8/7 is the smaller radius
x+16 = 8/7 + 16 = 8/7 + 112/7 = 120/7 is the larger radius
When converting each to a mixed number, we get:
8/7 = 1 & 1/7
120/7 = 17 & 1/7
Here are the approximate decimal values
8/7 = 1.142857
120/7 = 17.142857
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1203610: A 27 inches television has a 27 inches diagonal and a 16 inches width. What is the height of the 27 inches television? Round your answer to the nearest integer.
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1203444:
Found 2 solutions by greenestamps, Theo:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Apparently one of the tutors in preparing his response erased the original question....
But tutor @ikleyn repeated the question in her response, so I can see what the question was.
If E is the midpoint of DF, then DE (= DF - EF) is equal to EF. Given EF = x+9 and DF = 3x+9, we have
(3x+9)-(x+9) = x+9
2x = x+9
x = 9
And the length of DF is 3x+9 = 3(9)+9 = 27+9 = 36.
ANSWER: DF = 36
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you mentioned DF twice.
one of those menioned should be DE, rather than DF.
this leads to two interpretations.
i'll do both and you can decide which one you meant.
first interpretation:
E is the midpoint of DF. If EF = x + 9 and DE = 3x + 9, what is DF?
since E is the midpoint, then DE must be equal to EF.
this means that 3x + 9 = x + 9
subtract x from both sides of the equation and subtract 9 from both sides of the equation to get 2x = 0
solce for x to get x = 0
when x = 0, x + 9 = 9 and 3x + 9 = 9
this means that DE = 9 and EF = 9
since DF is the sum of its two line segments, then DF must be 18.
second interpretation.
E is the midpoint of DF. If EF = x + 9 and DF = 3x + 9, what is DE?
since E is the midpoint, then DE must be equal to EF.
this means that DE = EF.
since EF = x + 9, then DE must also be equal to x + 9.
you get:
DE + EF = DF becomes x + 9 + x + 9 = 3x + 9
combine like terms to get:
2x + 18 = 3x + 9
subtract 2x from both sides of the equation and subtract x from both sides of the equation to get:
9 = x
when x = 9, EF = 18
snce DE = EF, then DE = 18 also
you get:
18 + 18 = 3x + 9
combine like terms to get 36 = 3x + 9
since x = 9, you get 36 = 27 + 9 which becomes 36 = 36.
this confirms x = 9.
in the first interpretation, you were asked what is DF and the solution was DF = 18 and x = 0.
in the second interpretation, you werre asked what is DE and the solution was DE = 18 and x = 9.
we'll go through both interpretations again and see if the solutions make sense.
first interpretation:
E is the midpoint of DF. If EF = x + 9 and DE = 3x + 9, what is DF?
solution was DF = 18 and x = 0 *****
when x = 0, EF = 9 and DE = 9, you get 9 + 9 = 18, which is correct.
second interpretation:
E is the midpoint of DF. If EF = x + 9 and DF = 3x + 9, what is DE?
solution was DE = 18 and x = 9 *****
when x = 9 and DE = 18, you get 18 + 18 = 36, which is correct.
take your pick as to which of the interpretations you meant to provide.
your solution is the one associated with that interpretation.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925
|
| |






 .
.
 .
.
 .
.