Question 637354: How many 1 inch circles can be fit into an 8 inch square?
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20056)   (Show Source):
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! I assume the circles have a diameter of 1 inch and the square has a side length of 8 inches.
Mya answer is  circles, but I always have a long explanation.
The area (in square inches) of a circle with a 1-inch diameter (radius=1/2 inch) is
The area (in square inches) of a square with a side length of 8 inches is
If we could deform the circles into a more packing friendly shape, we could get
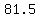  circles in the square.
That tells us that the answer will be less than that.
We may be tempted to make 8 rows of 8 circles to get 64 circles in, filling the square up like this:
 I know I did not draw all 64 circles, but you get the idea.
I can pack more if I alternate 8 circle layers and offset 7 circle layers as shown below. That way you can get 9 layers in: 5 layers of 8 circles, and 4 layers of 7 circles, for a total of 68 circles.
 Again, I got tired of drawing circles, so I left some out, but you get the idea.
The design has a 2-layer repeating pattern, and I calculated the heigh I neede for each 2-layer repeating pattern.
The way I calculated the packing of circles is by using those litle red triangles connecting the centers of circles in the drawing.
They are equilateral triangles, with a side length of 1 inch (same as the diameter of the circles.
Their height is  .
Two layers of those triangles, make a horizontal band with a height of  inches.
I just divided the height of the square by the height of that band;
 rounded.
That gave me hopes that I could fit 4 such bands between a bottom 0.5-inch band of half circles a top 0.5-inch band of half circles.
The height (in inches) of  -inch high bands was  .
The remaining height (8 inch - 6.98 inch = 1.1 inch) was enough for the top and bottom 0.5-inch layers, so I knew my design would fit.
I suspect there is no better way to pack those circles, but if you really want to know, maybe you can ask in the artofproblemsolving website forum. There are people there, with Math Olympics aspirations, who can solve almost any problem.
Most of them are smarter than at least 99% of us here.
|
|
|
