Question 1111549: Three circles C1,C2,C3 are externally tangent to each other. Center-to-center distances are 10 cm between C1 and C2 , 8 cm between C2 and C3 , and 6 cm between C3 and C1. Determine the total areas of the circles.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What you need is to find the radii of the circles.
When two circles touch externally, the distance between their center is the sum of their radii.
It gives you the system of three equations
a + b = 10, (1)
a + c = 8, (2)
b + c = 6. (3)
where a, b and c are the radii of the three circles with the centers A, B and C respectively.
To solve the system, first add all the three equations. You will get
2a + 2b + 2c = 10 + 8 + 6 = 24,
which implies
a + b + c = 12. (4)
Now subtract equation (3) from equation (4) (both sides). You will get c = 12-10 = 2.
Subtract equation (2) from equation (4) (both sides). You will get b = 12-8 = 4.
Finally, subtract equation (1) from equation (4) (both sides). You will get a = 12-6 = 6.
Now the area under the question is 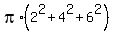 = 175.84 cm^2. = 175.84 cm^2.
---------------
To see similar solved problems, look into the lesson
- Three circles touching externally
in this site.
|
|
|