Question 1081620: Without graphing, Find the radius of a circle that is tangent to the y-axis that goes through two points (1,3), (2,4).
List the formulas you use and whether you solved for an specific variable in the formulas.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The equation of a circle is
 Since it's tangent to the y-axis, the center (h,k), is such that
its x-coordinate h = ħr, but since the given points are in the
first quadrant, the circle cannot go into the second quadrant and
be tangent to the y-axis. So h = r.
so we can substitute r for h
Since it's tangent to the y-axis, the center (h,k), is such that
its x-coordinate h = ħr, but since the given points are in the
first quadrant, the circle cannot go into the second quadrant and
be tangent to the y-axis. So h = r.
so we can substitute r for h

 Factor the left side as the difference of squares:
Factor the left side as the difference of squares:




 Substitute (x,y) = (1,3)
Substitute (x,y) = (1,3)


 Solve for 2r, that's the variable I solved for.
{No need to solve for r, for that would induce denominators)
Solve for 2r, that's the variable I solved for.
{No need to solve for r, for that would induce denominators)
 Substitute (x,y) = (2,4)
Substitute (x,y) = (2,4)


 Solve for 4r
Solve for 4r
 The system of equations to solve is
The system of equations to solve is
 Muliply both sides of the first equation by -2
to eliminate the r-terms
Muliply both sides of the first equation by -2
to eliminate the r-terms
 Adding the two equations term by term:
Adding the two equations term by term:

 k = 0; 4-k = 0
4 = k
Using k = 0
k = 0; 4-k = 0
4 = k
Using k = 0




 This is the graph of the circle with center (h,k)=(5,0) and radius r=5.
This is the graph of the circle with center (h,k)=(5,0) and radius r=5.
 Using k = 4
Using k = 4




 The radius cannot be negative. So there is only one solution
Edwin
The radius cannot be negative. So there is only one solution
Edwin
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Without graphing, Find the radius of a circle that is tangent to the y-axis that goes through two points (1,3), (2,4).
List the formulas you use and whether you solved for an specific variable in the formulas.
~~~~~~~~~~~~~~~~~~~~~~
The solution would be much easier to understand having a plot.
But, since you directly and explicitly ask do not graph, I will not use it.
Actually, there are TWO such circles as you will see later.
1. Draw (mentally) the segment connecting the given points (1,3) and (2,4).
This segment has the slope 1 = 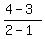 .
The centers of the two circles lie in the perpendicular bisector to this segment.
The perpendicular bisector goes through the middle point (1.5,3.5) and has the slope -1.
2. Let us find the radius of the "upper" circle.
Let "p" be the distance along the perpendicular bisector from the middle point (1.5,3.5) to the center of the "upper" circle.
Then the center of the "upper" circle is at the point ( .
The centers of the two circles lie in the perpendicular bisector to this segment.
The perpendicular bisector goes through the middle point (1.5,3.5) and has the slope -1.
2. Let us find the radius of the "upper" circle.
Let "p" be the distance along the perpendicular bisector from the middle point (1.5,3.5) to the center of the "upper" circle.
Then the center of the "upper" circle is at the point (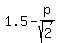 , ,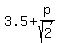 ), and the radius of the upper circle is ), and the radius of the upper circle is 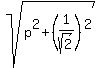 .
Since the upper circle touches y-axis, it gives the equation for "p" .
Since the upper circle touches y-axis, it gives the equation for "p"
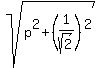 = = 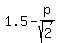 .
From this equation, p = (square both sides; simplify; then apply the quadratic formula) = .
From this equation, p = (square both sides; simplify; then apply the quadratic formula) =  .
Then the radius of the upper circle is .
Then the radius of the upper circle is  = =  = 1, which gives a = 1. (1)
The center of this circle is the point (1,4).
3. Now, let us find the radius of the "lower" circle.
Let "q" be the distance along the perpendicular bisector from the middle point (1.5,3.5) to the center of the "lower" circle.
Then the center of the "lower" circle is at the point ( = 1, which gives a = 1. (1)
The center of this circle is the point (1,4).
3. Now, let us find the radius of the "lower" circle.
Let "q" be the distance along the perpendicular bisector from the middle point (1.5,3.5) to the center of the "lower" circle.
Then the center of the "lower" circle is at the point (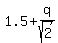 , ,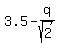 ), and the radius of the lower circle is ), and the radius of the lower circle is 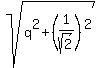 .
Since the lower circle touches y-axis, it gives the equation for "q" .
Since the lower circle touches y-axis, it gives the equation for "q"
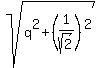 = = 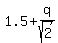 .
From this equation, q = (square both sides; simplify; then apply the quadratic formula) = .
From this equation, q = (square both sides; simplify; then apply the quadratic formula) = 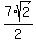 .
Then the radius of the upper circle is .
Then the radius of the upper circle is  = = 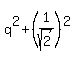 = = 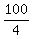 = 25, which gives b = = 25, which gives b =  = 5. (2)
The center of this circle is the point (5,0).
3. The equation for the "upper" circle is = 5. (2)
The center of this circle is the point (5,0).
3. The equation for the "upper" circle is
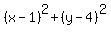 = 1.
The equation for the "lower" circle is = 1.
The equation for the "lower" circle is
 = 25. = 25.
Now, finally, I use all that I got and illustrate these results in the plot below.
It is my CHECK !

*** SOLVED ! ***
|
|
|