Tutors Answer Your Questions about Circles (FREE)
Question 540930: If we have 2 circles that intersect... each one attaching to the midpoint of the other circle, how do we explain using information about circle, why you know that the sides are all the same length.(Which would be a triangle drawn in the intersection between both circles) Please help me... Thank you :)
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If we have 2 circles that intersect... each one attaching to the midpoint of the other circle,
how do we explain using information about circle, why you know that the sides are all the same length.
(Which would be a triangle drawn in the intersection between both circles) Please help me... Thank you :)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As this "problem" is worded and presented, it is completely and totally nonsensical.
To a reader: if you happen to read this gibberish, ignore and skip it
and do not spend your time for nothing.
Question 563793: The larger circle circumscribes an equilateral triangle, which circumscribes a small circle. The area of the larger circle is 12pi. What is the triangle's perimeter. I not sure how to do this problem and how to work it out.
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The larger circle circumscribes an equilateral triangle, which circumscribes a small circle.
The area of the larger circle is 12pi. What is the triangle's perimeter.
I not sure how to do this problem and how to work it ou
~~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, the smaller circle is irrelevant, so we can omit any mention about it.
Therefore, I will reformulate the problem by removing everything that does not matter:
The circle circumscribes an equilateral triangle. The area of the circle is 12pi.
What is the triangle's perimeter ?
Below is the solution for this modified formulation.
For any triangle with the side lengths 'a', 'b' and 'c', the radius of the circumscribed circle is
R = 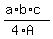 , (1)
where A is the area of the triangle. In our case, all three sides are congruent a = b = c,
so the radius of the circumscribed circle is
R = , (1)
where A is the area of the triangle. In our case, all three sides are congruent a = b = c,
so the radius of the circumscribed circle is
R = 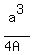 . (2)
The area of the circumscribed circle is A = . (2)
The area of the circumscribed circle is A = 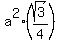 square units.
Substituting it into the formula (1), we get
R = square units.
Substituting it into the formula (1), we get
R = 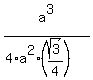 = = 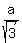 . (3)
We are given that the area of the circle is . (3)
We are given that the area of the circle is 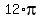 , so we can write this equation , so we can write this equation
 = = 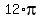 .
Cancel .
Cancel  in both sides to get in both sides to get
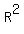 = 12.
Substitute here R from (3). You will get = 12.
Substitute here R from (3). You will get
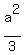 = 12.
Simplify and find 'a' = 12.
Simplify and find 'a'
 = 3*12 = 36, a = = 3*12 = 36, a = 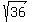 = 6 units.
Hence, the perimeter of the triangle is 3*6 = 18 units.
ANSWER. The perimeter of the triangle is 18 units. = 6 units.
Hence, the perimeter of the triangle is 3*6 = 18 units.
ANSWER. The perimeter of the triangle is 18 units.
Thus we produced short, straightforward, compact and elegant Geometry solution.
Question 1202895: 15. The original "Ferris" wheel, designed by George Washington Gale Ferris Jr., was built for the World's Columbian Exposition of 1893 in Chicago, Illinois. There were 36 fully enclosed gondolas (passenger cars) that carried up to 40 passengers.
This "Ferris" wheel eventually left Chicago and was relocated in St. Louis, Missouri in time for the 1904 Louisiana Purchase Exposition. On May 11, 1906, it was demolished using a dynamite charge and sold for scraps.
The circumference of the "Ferris" wheel had to be large enough to allow for an arc length of 20.64 ft between each gondola. What was the circumference of the original "Ferris" wheel? Round to the nearest whole number.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The original "Ferris" wheel, designed by George Washington Gale Ferris Jr., was built for the World's Columbian Exposition
of 1893 in Chicago, Illinois. There were 36 fully enclosed gondolas (passenger cars) that carried up to 40 passengers.
This "Ferris" wheel eventually left Chicago and was relocated in St. Louis, Missouri in time for the 1904 Louisiana
Purchase Exposition. On May 11, 1906, it was demolished using a dynamite charge and sold for scraps.
The circumference of the "Ferris" wheel had to be large enough to allow for an arc length of 20.64 ft between each gondola.
What was the circumference of the original "Ferris" wheel? Round to the nearest whole number.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Actually, as it is presented/printed in the post, this problem can not be solved
and the question can not be answered correctly, until the length of each gondola is given.
But it can be, that the goal of a problem composer was to force a reader
to solve the problem, assuming the zero length of gondolas.
If it is so, then I am very shocked to see this solution by @Theo, as long as 14 lines of arguments.
The true solution is much shorter, in one or two lines.
We have 20 arcs, each of 20.64 ft long (along the circumference, as the problem says).
Then the circumference is simply 20*20.64 = 743.04 ft. <<<---=== ANSWER
Solved.
----------------------
This "problem" is somewhere between a Math joke and Math stupidity, but closer to Math stupidity.
It contains many words to confuse a reader and to distract his/her attention, but does not contain
vitally important information, which is necessary for solution.
So, the problem's composer not only confuses a reader - - - he/she confuses himself (or herself), too.
I've seen this problem and its duplicates on several other websites.
So, some "thinkers" actively disseminate this gibberish online
instead of throwing it to the trash bin, where its right place should be.
What is strange to me is the fact that other tutors consider this "problem" seriously
and do not see that it is defective.
I have not seen (unfortunately) any qualified tutor expose this problem as invalid.
So, I am first who says "the king is naked".
"The king is naked" refers to "The Emperor's New Clothes," a famous fairy tale by Hans Christian Andersen
about a vain emperor tricked into believing he is wearing invisible, magnificent clothes that are only visible
to the wise. In truth, he is naked, but his courtiers and the townspeople remain silent, afraid of being
thought foolish. The deception is revealed when a child innocently shouts the truth, "The king is naked!".
The story serves as a metaphor for how fear, pride, and conformity prevent people
from speaking truth to power, and how a child's innocence can cut through widespread delusion.
Question 1210387: A television tower broadcasts its signal at a range of 18.1 miles from the tower to its further point. How many square miles are covered by the range of this tower? Round your answer to the nearest hundredth if necessary.
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1167805: The figure below shows two pulleys of radii 6cm and 4cm with centres A and B respectively. AB = 8cm. The pulleys are connected by a string PQXRSY
https://www.easyelimu.com/images/topicalrevision/maths/form_3/circles_chords_and_tangents/circle_q5.PNG
calculate
(a) Length PQ
(b) PAS reflex
(c) Length of arc PYS and QXR
(d) The total length of the string PQXRSY
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Regarding this post and the " solution " by @CPhill, I have two notices.
(1) The plot in the attached file does not correspond / (is not adequate) to the given data.
Indeed, if the radii are 6 cm and 4 cm and the circles do not overlay,
then the distance between the centers can not be less than 6 + 4 = 10 cm,
but with the given data the relevant distance is less than 10 cm.
(2) The solution in the post by @CPhill is INCORRECT.
Indeed, in his solution, @CPhill considers the distance of 8 cm long
as the hypotenuse of the right angled triangle.
But it is incorrect. This distance of 8 cm is one of the LEGS of the right-angled triangle.
Therefore, all that follows in the solution by @CPhill is WRONG.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solutions are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's a step-by-step calculation for each part of the problem based on the provided figure and common geometry principles for pulleys and tangents.
First, let's define the radii and distance between centers:
* Radius of pulley A ($R_A$) = 6 cm
* Radius of pulley B ($R_B$) = 4 cm
* Distance between centers AB ($d$) = 8 cm
We will use a reference angle $\theta$ for calculations related to the tangent lines. This angle is formed by the line connecting the centers (AB) and the radius to the tangent point (e.g., AP).
In the right-angled triangle formed by drawing a line from the center of the smaller pulley (B) perpendicular to the radius of the larger pulley (AP), let's call the intersection point L.
The sides of this triangle are:
* Hypotenuse = AB = 8 cm
* Side adjacent to $\angle BAL$ = $AL = R_A - R_B = 6 - 4 = 2$ cm.
Therefore, $\cos(\angle BAL) = \frac{AL}{AB} = \frac{2}{8} = \frac{1}{4}$.
Let $\theta = \angle BAL = \arccos(1/4)$ radians.
Numerically, $\theta \approx 1.3181$ radians (or $75.52^\circ$).
---
**(a) Calculate Length PQ**
The length of the common external tangent (PQ) can be found using the Pythagorean theorem:
$PQ = \sqrt{d^2 - (R_A - R_B)^2}$
$PQ = \sqrt{8^2 - (6 - 4)^2}$
$PQ = \sqrt{64 - 2^2}$
$PQ = \sqrt{64 - 4}$
$PQ = \sqrt{60} = \sqrt{4 \times 15} = 2\sqrt{15}$ cm.
**Length PQ = $2\sqrt{15}$ cm**
---
**(b) PAS reflex**
The angle $\theta = \arccos(1/4)$ is the angle formed by the line of centers AB and the radius AP (or AS).
Due to the symmetry of the tangents, the angle $\angle PAB = \theta$ and $\angle SAB = \theta$.
So, the smaller angle $\angle PAS = 2\theta = 2\arccos(1/4)$ radians.
The question asks for the **reflex** angle PAS. This is the larger angle around center A.
Reflex $\angle PAS = 2\pi - 2\theta$ radians.
In degrees: $360^\circ - (2 \times 75.52^\circ) = 360^\circ - 151.04^\circ = 208.96^\circ$.
**PAS reflex = $2\pi - 2\arccos(1/4)$ radians (or approximately $208.96^\circ$)**
---
**(c) Length of arc PYS and QXR**
* **Length of arc PYS (on pulley A):**
This arc is on the larger pulley with radius $R_A = 6$ cm. The central angle for this arc is the reflex angle PAS calculated in part (b).
Arc length $L_{PYS} = R_A \times (\text{Reflex } \angle PAS \text{ in radians})$
$L_{PYS} = 6 \times (2\pi - 2\arccos(1/4))$ cm.
$L_{PYS} = 12(\pi - \arccos(1/4))$ cm.
* **Length of arc QXR (on pulley B):**
This arc is on the smaller pulley with radius $R_B = 4$ cm. From the diagram, arc QXR is the minor arc.
The central angle for arc QXR is formed by radii BQ and BR. In the context of direct tangents, the angle for the minor arc is $\pi - 2\theta$, where $\theta = \arccos(1/4)$.
Arc length $L_{QXR} = R_B \times (\pi - 2\theta)$ radians.
$L_{QXR} = 4 \times (\pi - 2\arccos(1/4))$ cm.
**Length of arc PYS = $12(\pi - \arccos(1/4))$ cm**
**Length of arc QXR = $4(\pi - 2\arccos(1/4))$ cm**
---
**(d) The total length of the string PQXRSY**
The total length of the string is the sum of the two straight tangent segments (PQ and RS) and the two arc lengths (PYS and QXR).
Due to symmetry, $PQ = RS$.
Total Length = $2 \times PQ + L_{PYS} + L_{QXR}$
Total Length = $2 \times (2\sqrt{15}) + 12(\pi - \arccos(1/4)) + 4(\pi - 2\arccos(1/4))$
Total Length = $4\sqrt{15} + 12\pi - 12\arccos(1/4) + 4\pi - 8\arccos(1/4)$
Total Length = $4\sqrt{15} + 16\pi - 20\arccos(1/4)$ cm.
**The total length of the string PQXRSY = $4\sqrt{15} + 16\pi - 20\arccos(1/4)$ cm**
---
**Numerical Approximations (for reference, if needed):**
* $\sqrt{15} \approx 3.873$
* $\pi \approx 3.1416$
* $\arccos(1/4) \approx 1.3181$ radians
* Length PQ $\approx 2 \times 3.873 = 7.746$ cm.
* Reflex PAS $\approx 2\pi - 2(1.3181) = 6.2832 - 2.6362 = 3.6470$ radians.
* $L_{PYS} \approx 6 \times 3.6470 = 21.882$ cm.
* $L_{QXR} \approx 4 \times (\pi - 2 \times 1.3181) = 4 \times (3.1416 - 2.6362) = 4 \times 0.5054 = 2.022$ cm.
* Total Length $\approx (2 \times 7.746) + 21.882 + 2.022 = 15.492 + 21.882 + 2.022 = 39.396$ cm.
Question 1176479: Given seven equal circles on a hexagonal grid, how many permutations are possible where circles are always adjacent (repetitions such as inversions and reflections excluded)?
Thank you.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given seven equal circles on a hexagonal grid, how many permutations are possible where circles
are always adjacent (repetitions such as inversions and reflections excluded)?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
I have another logic/reasoning, and my solution and my answer are different from that by @CPhill.
But before to start, I'd like to discuss the problem's formulation.
The problem says
Given seven equal circles on a hexagonal grid, how many permutations are possible where circles
are always adjacent (repetitions such as inversions and reflections excluded)?
I would re-formulate the problem in mathematically more appropriate way:
Given seven equal circles on a hexagonal grid, how many arrangements are possible where circles
are always adjacent (arrangements that differ by rotations, inversions, and reflections
are considered as indistinguishable).
Below is my solution for this modified formulation.
S O L U T I O N
We consider 7 circles as numbered from 1 to 7 - so the circles are distinguishable.
To start, let assume that the circle '7' is in the center.
Then, accounting for circular permutations (rotations), we have (6-1)! = 5! = 120 different arrangements.
There are 3 different axes of symmetry.
To account for reflections, we divide the number of 120 arrangements by 2 three times.
We get then 120 : 8 = 15 distinguishable arrangements.
We should not make an additional correction for inversion, since the inversion
is just accounted as the 180-degree rotation.
So, now we only need to multiply 15 by 7 to account for the fact that any of 7 circles can be placed in the center.
ANSWER. Under the given conditions (and with my modification) there are 15*7 = 105 different distinguished arrangements.
Solved.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step.
**Understanding the Problem**
We have seven equal circles arranged on a hexagonal grid. The arrangement forms a central circle with six circles surrounding it. We want to find the number of unique permutations of these circles, where adjacency is maintained, and rotations and reflections are considered the same permutation.
**Visualizing the Arrangement**
Imagine the circles arranged like this:
```
O
O O
O O
O O
O
```
Where the center "O" is surrounded by six other "O"s.
**Finding Permutations**
1. **Start with the Central Circle:** The central circle is fixed. We only need to arrange the six surrounding circles.
2. **Permutations of the Outer Circles:** If the outer circles were distinct, there would be 6! (6 factorial) permutations, which is 6 * 5 * 4 * 3 * 2 * 1 = 720.
3. **Accounting for Rotations:** Since rotations are considered the same, we need to divide by the number of rotations. There are 6 rotations (0°, 60°, 120°, 180°, 240°, 300°), so we divide 6! by 6:
* 720 / 6 = 120
4. **Accounting for Reflections:** We also need to account for reflections. In this case, there are 6 lines of reflection symmetry. We already accounted for rotations, so we need to divide by 2 to account for the reflections.
* 120 / 2 = 60
**Therefore, there are 60 unique permutations of the circles.**
Question 1177001: EVOL is a cyclic quadrilateral, inscribed in a circle with center S. Given that the radius of this circle is 25 in. and angle VEL is 55 degrees, explain your work to find the following measurements.
a)Length of Major Arc VL
b)Angle measure of Minor Arc VL
c)Angle VOL
d)Length of Chord VL
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52852)   (Show Source): (Show Source):
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's break down this geometry problem step-by-step.
**Understanding the Setup**
* **EVOL is a cyclic quadrilateral:** This means all four vertices (E, V, O, L) lie on the circumference of a circle.
* **Center S:** The center of the circle is denoted as S.
* **Radius = 25 in:** The distance from S to any point on the circle is 25 inches.
* **∠VEL = 55 degrees:** This is an inscribed angle.
**Solving the Problem**
**a) Length of Major Arc VL**
1. **Angle VOL (Central Angle):**
* In a cyclic quadrilateral, opposite angles are supplementary (add up to 180 degrees). However we do not need that fact for this part of the problem.
* The measure of a central angle is twice the measure of an inscribed angle that subtends the same arc.
* Therefore, ∠VOL = 2 * ∠VEL = 2 * 55 degrees = 110 degrees. This is the measure of the minor arc VL.
* The major arc VL is 360 degrees - 110 degrees = 250 degrees.
2. **Circumference:**
* The circumference of the circle is C = 2 * π * r = 2 * π * 25 = 50π inches.
3. **Length of Major Arc VL:**
* The length of the major arc is the fraction of the circumference corresponding to the central angle of the major arc.
* Length of major arc VL = (250/360) * 50π = (25/36) * 50π = (1250π/36) = (625π/18) inches.
**b) Angle Measure of Minor Arc VL**
* As calculated in part (a), the measure of minor arc VL is equal to the central angle that subtends it, which is ∠VOL.
* Therefore, the angle measure of minor arc VL is 110 degrees.
**c) Angle VOL**
* We already calculated this in part (a).
* ∠VOL = 110 degrees.
**d) Length of Chord VL**
1. **Triangle VOL:**
* Triangle VOL is an isosceles triangle because SV = SL = 25 inches (both are radii).
* We know angle VOL is 110 degrees.
2. **Law of Cosines:**
* We can use the Law of Cosines to find the length of chord VL:
* VL² = VO² + LO² - 2 * VO * LO * cos(∠VOL)
* VL² = 25² + 25² - 2 * 25 * 25 * cos(110°)
* VL² = 625 + 625 - 1250 * cos(110°)
* VL² = 1250 - 1250 * (-0.3420)
* VL² = 1250 + 427.5
* VL² = 1677.5
* VL = √1677.5 ≈ 40.96 inches.
**Summary of Answers**
* **a) Length of Major Arc VL:** 625π/18 inches (approximately 109.08 inches)
* **b) Angle Measure of Minor Arc VL:** 110 degrees
* **c) Angle VOL:** 110 degrees
* **d) Length of Chord VL:** Approximately 40.96 inches
Question 1209532: Point R is chosen on the circumference of a circle and arc PQ is drawn with R as its center. If P and Q are joined, the line segment formed is a diameter of the circle with length 2r cm. Find the area of the shaded region in terms of r, in square centimeters.
Link to diagram: https://ibb.co/GQFdy2SV
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52852)   (Show Source): (Show Source):
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the area of the shaded region:
1. **Area of the Semicircle:** Since PQ is the diameter, the radius of the circle is r. The area of the entire circle is πr², so the area of the semicircle (the region above PQ) is (1/2)πr².
2. **Area of Triangle PQR:** Triangle PQR is inscribed in a semicircle with PQ as the diameter. A fundamental theorem states that any triangle inscribed in a semicircle with the diameter as one side is a right triangle. Therefore, angle PRQ is a right angle.
* The base of triangle PQR is PQ (the diameter), which has a length of 2r.
* The height of triangle PQR is the perpendicular distance from R to PQ. Since R is on the circle's circumference, this height is equal to the radius, r.
* Area of triangle PQR = (1/2) * base * height = (1/2) * 2r * r = r²
3. **Area of the Shaded Region:** The shaded region is the area of the semicircle *minus* the area of triangle PQR.
Shaded Area = Area of Semicircle - Area of Triangle PQR
Shaded Area = (1/2)πr² - r²
4. **Simplify:** We can factor out r²:
Shaded Area = r² * [(π/2) - 1]
Therefore, the area of the shaded region is **r²[(π/2) - 1]** square centimeters.
Question 1209524: (46) Sector ABC is 1/12 of a circle with diameter 24k. Line segment AD is perpendicular to segment BC. Find the area of the shaded region.
Link to diagram: https://ibb.co/5gNwX0K6
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Sector ABC is 1/12 of a circle with diameter 24k. Line segment AD is perpendicular to segment BC.
Find the area of the shaded region.
Link to diagram: https://ibb.co/5gNwX0K6
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill is INCORRECT.
I came to bring a correct solution.
We should take the area of the sector ABC and subtract from it the area of triangle ABD.
The area of the sector ABC is 1/12 of the area of the circle
area of the sector ABC is  = = 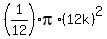 = = 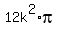 . (1)
Triangle ABD has the angle B = 30°.
So, its leg AD is 12k/2 = 6k long;
leg BD is . (1)
Triangle ABD has the angle B = 30°.
So, its leg AD is 12k/2 = 6k long;
leg BD is  .
The area of triangle ABD is half the product of the legs
area ABD = .
The area of triangle ABD is half the product of the legs
area ABD = 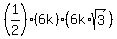 = =  . (2)
Thus the area of the shaded region is the difference (1) minus (2)
area of the shaded region is . (2)
Thus the area of the shaded region is the difference (1) minus (2)
area of the shaded region is  = =  ,
or approximately ,
or approximately  = =  . .
Solved.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
. . . . . . . . . . . . . . . . . . . . . . . .
I reviewed many geometric problems, where @CPhill (= artificial intelligence) produced wrong solutions.
My resume from my reviews to these solutions is that this AI in its current version
is MENTALLY BLIND regarding Geometry problems.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break the problem down step by step:
### **Step 1: Determine the Radius of the Circle**
- The given diameter of the circle is \( 24k \), so the radius is:
\[
r = \frac{24k}{2} = 12k
\]
### **Step 2: Compute the Area of Sector ABC**
- The full circle has an area of:
\[
A_{\text{circle}} = \pi r^2 = \pi (12k)^2 = 144\pi k^2
\]
- Since sector ABC is \( \frac{1}{12} \) of the full circle, its area is:
\[
A_{\text{sector}} = \frac{1}{12} \times 144\pi k^2 = 12\pi k^2
\]
### **Step 3: Find the Area of Triangle ABD**
- Since \( AD \) is perpendicular to \( BC \), we assume \( AD \) is the height of \( \triangle ABC \), where \( BC \) is the chord of the sector.
- The central angle of the sector is:
\[
\theta = \frac{360^\circ}{12} = 30^\circ
\]
- The triangle \( \triangle ABC \) is an isosceles triangle with two equal sides being the radii \( 12k \), and the included angle \( 30^\circ \).
- Using the formula for the area of a triangle:
\[
A_{\triangle ABC} = \frac{1}{2} r^2 \sin \theta
\]
\[
= \frac{1}{2} (12k)^2 \sin 30^\circ
\]
\[
= \frac{1}{2} (144k^2) \times \frac{1}{2}
\]
\[
= \frac{144k^2}{4} = 36k^2
\]
### **Step 4: Compute the Shaded Region**
- The shaded area is the sector minus the triangle:
\[
A_{\text{shaded}} = A_{\text{sector}} - A_{\triangle ABC}
\]
\[
= 12\pi k^2 - 36k^2
\]
\[
= 36k^2 (\pi - 1)
\]
Thus, the area of the shaded region is:
\[
\boxed{36k^2 (\pi - 1)}
\]
Question 1210278: How to solve slant height of a cone
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1168234: Find the general equation of the circle, if the circle is tangent to the line -3x+2y+1=0 at the point (1, 1), and the center is on the line x+y-1=0.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the general equation of the circle,
if the circle is tangent to the line  at the point ( at the point ( , ,  ), then radius on the line ), then radius on the line  is perpendicular to tangent line is perpendicular to tangent line
so,


hence, 
perpendicular line containing radius, will have a slope:

 ......plug in m and the point ( ......plug in m and the point ( , ,  ) )




the center ( , ,  ) is the point of intersection of perpendicular line and ) is the point of intersection of perpendicular line and 
 .........eq.1 .........eq.1
 .............eq.2 .............eq.2
-----------------------

substitute in eq.1






intersection point is ( , ,  ) )
so, ( , ,  ) =( ) =( , ,  ) )
 , , 
Length of radius  = distance from line = distance from line  to center ( to center ( , ,  ) and it is ) and it is

the equation of the circle




Question 1168232: A circle is centered at (2,1) and tangent to the line x+y=0.
(a) find the equation of the circle
(b) find the area and circumference of the circle.
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1168231: Find the equation of a circle is tangent to the line -x+y+4=0 at the point (3, -1), and the center is on (1, 1).
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1209844:
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The problem was posted in absolutely inacceptable format, so I deleted the post.
Please do not post GIBBERISH to this forum - otherwise, I will re-direct it into a garbage bin,
immediately, instantly and without explanations.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this geometry problem step-by-step.
**Understanding the Problem**
* We are given a circle with points F, G, Q, and R on its circumference.
* We are given the measures of arcs FG and FQ.
* We are given that FR = FG.
* We need to find the measure of angle RPG.
**Solving the Problem**
1. **Measure of Arc GR:**
* Since FR = FG, the arcs FR and FG are equal in measure.
* Therefore, the measure of arc FR is also 118°.
* The measure of arc GR is the difference between the measure of arc FR and the measure of arc FG:
* Measure of arc GR = 118° - 118° = 0°.
* This means that R and G are the same point. There is an error in the provided image. R and G can not be the same point, so there is likely a typo in the problem. I will continue the problem as if R and G are different points.
* Measure of arc QR = measure of arc FR - measure of arc FQ = 118-25 = 93.
2. **Measure of Angle QPR:**
* Angle QPR is an exterior angle formed by secants KQ and RM.
* The measure of an exterior angle formed by secants is half the difference of the intercepted arcs.
* Measure of angle QPR = 1/2 (measure of arc QR - measure of arc FG)
* Measure of angle QPR = 1/2 (93° - 118°)
* This result is negative, which means that the points are labelled incorrectly.
* Therefore, we must use the difference of the larger arc and the smaller arc, in that order. So we will use the absolute value.
* Measure of angle QPR = 1/2 |measure of arc FG - measure of arc FQ|
* Measure of angle QPR = 1/2 |118 - 25| = 1/2(93) = 46.5.
* Measure of angle QPR= 46.5 degrees.
3. **Measure of Angle RPG:**
* Angle RPG is the same as angle QPR.
* Therefore, the measure of angle RPG is 46.5 degrees.
**Answer**
The measure of angle RPG is 46.5 degrees.
Question 1209799: 1. 137+6y=-y^2-x^2-24x
2. x^2+y^2+14x-12y+4=0
3. y^2+2x+x^2=24y-120
4. x^2+2x+y^2=55+10y
5. 8x+32y+y^2=-263-x^2
Found 2 solutions by CPhill, timofer:
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! The provided equations are not in the standard form of a circle, which is (x - h)^2 + (y - k)^2 = r^2, where (h, k) is the center and r is the radius. I'll first convert them to the standard form and then plot them using Altair.
1. **137 + 6y = -y^2 - x^2 - 24x**
Rearranging the terms, we get x^2 + 24x + y^2 + 6y = -137
Completing the square for x, we add (24/2)^2 = 144 to both sides: x^2 + 24x + 144 + y^2 + 6y = -137 + 144
Completing the square for y, we add (6/2)^2 = 9 to both sides: x^2 + 24x + 144 + y^2 + 6y + 9 = -137 + 144 + 9
Simplifying, we get (x + 12)^2 + (y + 3)^2 = 16 = 4^2
So, the center is (-12, -3) and the radius is 4.
2. **x^2 + y^2 + 14x - 12y + 4 = 0**
Rearranging the terms, we get x^2 + 14x + y^2 - 12y = -4
Completing the square for x, we add (14/2)^2 = 49 to both sides: x^2 + 14x + 49 + y^2 - 12y = -4 + 49
Completing the square for y, we add (-12/2)^2 = 36 to both sides: x^2 + 14x + 49 + y^2 - 12y + 36 = -4 + 49 + 36
Simplifying, we get (x + 7)^2 + (y - 6)^2 = 81 = 9^2
So, the center is (-7, 6) and the radius is 9.
3. **y^2 + 2x + x^2 = 24y - 120**
Rearranging the terms, we get x^2 + 2x + y^2 - 24y = -120
Completing the square for x, we add (2/2)^2 = 1 to both sides: x^2 + 2x + 1 + y^2 - 24y = -120 + 1
Completing the square for y, we add (-24/2)^2 = 144 to both sides: x^2 + 2x + 1 + y^2 - 24y + 144 = -120 + 1 + 144
Simplifying, we get (x + 1)^2 + (y - 12)^2 = 25 = 5^2
So, the center is (-1, 12) and the radius is 5.
4. **x^2 + 2x + y^2 = 55 + 10y**
Rearranging the terms, we get x^2 + 2x + y^2 - 10y = 55
Completing the square for x, we add (2/2)^2 = 1 to both sides: x^2 + 2x + 1 + y^2 - 10y = 55 + 1
Completing the square for y, we add (-10/2)^2 = 25 to both sides: x^2 + 2x + 1 + y^2 - 10y + 25 = 55 + 1 + 25
Simplifying, we get (x + 1)^2 + (y - 5)^2 = 81 = 9^2
So, the center is (-1, 5) and the radius is 9.
5. **8x + 32y + y^2 = -263 - x^2**
Rearranging the terms, we get x^2 + 8x + y^2 + 32y = -263
Completing the square for x, we add (8/2)^2 = 16 to both sides: x^2 + 8x + 16 + y^2 + 32y = -263 + 16
Completing the square for y, we add (32/2)^2 = 256 to both sides: x^2 + 8x + 16 + y^2 + 32y + 256 = -263 + 16 + 256
Simplifying, we get (x + 4)^2 + (y + 16)^2 = 9 = 3^2
So, the center is (-4, -16) and the radius is 3.
Now, I'll use Altair to plot these circles.
```python
import altair as alt
import pandas as pd
import numpy as np
# Define the center and radius of each circle
circles = [
{'center': (-12, -3), 'radius': 4, 'name': 'Circle 1'},
{'center': (-7, 6), 'radius': 9, 'name': 'Circle 2'},
{'center': (-1, 12), 'radius': 5, 'name': 'Circle 3'},
{'center': (-1, 5), 'radius': 9, 'name': 'Circle 4'},
{'center': (-4, -16), 'radius': 3, 'name': 'Circle 5'}
]
# Create a list to hold the data for all circles
all_circles_data = []
for circle in circles:
# Generate points on the circle circumference
theta = np.linspace(0, 2 * np.pi, 100)
x_circ = circle['center'][0] + circle['radius'] * np.cos(theta)
y_circ = circle['center'][1] + circle['radius'] * np.sin(theta)
# Create a DataFrame for the circle data
circle_data = pd.DataFrame({
'x': x_circ,
'y': y_circ,
'Circle': circle['name']
})
all_circles_data.append(circle_data)
# Concatenate all circle DataFrames into a single DataFrame
all_circles_df = pd.concat(all_circles_data)
# Create the Altair chart
chart = alt.Chart(all_circles_df).mark_circle().encode(
x=alt.X('x', axis=alt.Axis(title='X-axis')),
y=alt.Y('y', axis=alt.Axis(title='Y-axis')),
color='Circle', # Use color to differentiate circles
tooltip=['Circle', 'x', 'y']
).properties(
title='Circle Plots'
)
# Save the chart
chart.save('circle_plots.json')
```
This code will generate a JSON file that can be opened in any web browser to view the interactive plot of the circles.
Answer by timofer(105)  (Show Source): (Show Source):
You can put this solution on YOUR website! Use the previous response which was for your equation 1 here. You want to complete the squares if necessary and put equation into the needed form. Decide then what it is or make the graph.
Question 1209798: 137+6y=-y^2-x^2-24x
Found 2 solutions by timofer, josgarithmetic:
Answer by timofer(105)  (Show Source): (Show Source):
You can put this solution on YOUR website! You should try to complete the square for the x and the y and simplify. You will need 144 for the x and need 9 for the y.
This is the equation you can expect.

Answer by josgarithmetic(39625)  (Show Source): (Show Source):
You can put this solution on YOUR website! what do you want with this? It appears it might be a circle, but that depends on what happens when you try to adjust the form of the equation.
Question 1209526: (55) Equilateral triangle ABC, with a side of length 4, is inscribed in a circle. The midpoint of AB is D and the midpoint of AC is E. If DE is extended to meet the circle at F, find the length of EF.
Link to diagram: https://ibb.co/6czn24rm
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(55) Equilateral triangle ABC, with a side of length 4, is inscribed in a circle.
The midpoint of AB is D and the midpoint of AC is E. If DE is extended to meet
the circle at F, find the length of EF.
Link to diagram: https://ibb.co/6czn24rm
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Point F is obtained by extending DE to intersection with the circle.
Extend DE in the opposite direction to intersection with the circle in point G.
Then, due to symmetry, EF = DG.
Let x be the length of EF.
Now we have two intersecting chords GF and AC, and we are going to apply the theorem
about intersecting chords.
The intersection point E divides chord AC in two equal intervals, AE = EC = 4/2 = 2 units long, each.
The intersection point E divides chord GF in two intervals, EF = x and GE = 2+x units long.
Now apply the theorem about intersecting chords
AE * EC = GE * EF,
or
2*2 = (2+x)*x.
Simplify and find x from this equation
4 = 2x + x^2,
x^2 + 2x - 4 = 0,
 = = 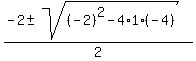 = = 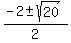 = = 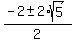 = = 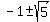 .
We reject the negative root and keep the positive root.
Thus we get the
ANSWER. The length of EF is .
We reject the negative root and keep the positive root.
Thus we get the
ANSWER. The length of EF is  = 1.2361 units (approximately). = 1.2361 units (approximately).
Solved.
Good problem, I enjoyed solving it.
Question 1209525: (49) In the diagram, ABCD is a unit square. Arc AC has center D and arc BD has center C. Find the shaded area in square units.
Link to diagram: https://ibb.co/zhCbbmhz
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1209521: (42) Two circles of unit radius with centers A and B are tangent to each other at C. They are also tangent internally to a circle with center C. Find the area of the shaded region.
Link to diagram: https://ibb.co/QFchDRT5
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1209274: A tractor has a rear wheel with a circumference of x m. The circumference of the front wheel is 5 m less. If the front wheel makes 15 more revolutions than the rear wheel every 450 m, what is the circumference, in m, of the front wheel?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 10 meters
Explanation
x = circumference of rear wheel
x-5 = circumference of front wheel
Each measurement is in meters.
Each value is a positive real number.
x-5 > 0 leads to x > 5
So if any x value 5 or smaller shows up, we simply ignore it.
The goal is to compute x-5.
One revolution of the rear wheel will mean that it travels x meters because it's the perimeter of the wheel.
This assumes the wheel does not slip.
Two revolutions, the wheel travels 2x meters.
Three revolutions, the wheel travels 3x meters.
And so on.
After traveling 450 meters, the rear wheel makes 450/x revolutions.
Meanwhile the front wheel makes 450/(x-5) revolutions which is 15 more compared to the previous amount.
(450/x) + 15 = 450/(x-5)
x(x-5)*( (450/x) + 15 ) = x*(x-5)*( 450/(x-5) )
450(x-5) + 15x(x-5) = 450x
450x-2250 + 15x^2-75x = 450x
450x-2250 + 15x^2-75x - 450x = 0
15x^2 - 75x - 2250 = 0
15(x^2 - 5x - 150) = 0
x^2 - 5x - 150 = 0
(x+10)(x-15) = 0
x+10 = 0 or x-15 = 0
x = -10 or x = 15
Ignore the negative value since we stated earlier that x > 5.
If the real wheel has circumference x = 15 meters then it makes 450/x = 450/15 = 30 revolutions in the 450 meter distance.
Meanwhile the front wheel makes 450/(x-5) = 450/(15-5) = 45 revolutions which is 15 more compared to the previous value.
This helps verify we have the correct x value.
Then the last thing to do is compute x-5 to get x-5 = 15-5 = 10 meters as the circumference of the front wheel.
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A tractor has a rear wheel with a circumference of x m. The circumference of the front wheel is 5 m less.
If the front wheel makes 15 more revolutions than the rear wheel every 450 m,
what is the circumference, in m, of the front wheel?
~~~~~~~~~~~~~~~~~~
The rear wheel has the circumference of x meters.
Hence, the front wheel has the circumference of (x-5) meters, according to the problem.
The rear wheel makes  rotations every 450 m.
The front wheel makes rotations every 450 m.
The front wheel makes  rotations every 450 m.
The problem says rotations every 450 m.
The problem says
 - -  = 15.
It is your setup equation.
To solve it, first multiply both sides by x*(x-5); then simplify
450x - 450(x-5) = 15x(x-5)
450x - 450x + 2250 = 15x(x-5)
2250 = 15x(x-5)
150 = x*(x-5).
At this point, you may guess that x = 15.
Indeed, 15*(15-5) = 15*10 = 150.
In addition, the function x*(x-5) is monotonic at x > 5,
so, this guessed solution is UNIQUE in the domain x > 5.
Alternatively, you may solve equation x^2 - 5x - 150 = 0 factoring or by using
the quadratic formula.
So, the circumstance of the rear wheel is 15 meters.
Hence, the circumstance if the front wheel is 15-5 = 10 meters. ANSWER = 15.
It is your setup equation.
To solve it, first multiply both sides by x*(x-5); then simplify
450x - 450(x-5) = 15x(x-5)
450x - 450x + 2250 = 15x(x-5)
2250 = 15x(x-5)
150 = x*(x-5).
At this point, you may guess that x = 15.
Indeed, 15*(15-5) = 15*10 = 150.
In addition, the function x*(x-5) is monotonic at x > 5,
so, this guessed solution is UNIQUE in the domain x > 5.
Alternatively, you may solve equation x^2 - 5x - 150 = 0 factoring or by using
the quadratic formula.
So, the circumstance of the rear wheel is 15 meters.
Hence, the circumstance if the front wheel is 15-5 = 10 meters. ANSWER
Solved.
You may check the answer on your own, by substituting the numbers into the problem.
Question 1208994: An archery target is constructed of five concentric circles such that the area of the inner circle is equal to the area of each of the four rings. If the radius of the outer circle is 12 m, then the width of band a, in m.
https://ibb.co/h78NMWQ
I am very confused as to which band is a and what method to use for this
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! An archery target is constructed of five concentric circles such that the area of the inner circle
is equal to the area of each of the four rings. If the radius of the outer circle is 12 m, then
 the width of band a, in m. the width of band a, in m.
https://ibb.co/h78NMWQ
I am very confused as to which band is a and what method to use for this
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
We have one circle and four rings: in all, 1 + 4 = 5 shapes of equal areas.
The area of the outer circle is  = =  .
The area of each shape is 1/5 of the total area,
since the partial areas of all shapes are equal to each other.
They want you find the width of the band for the ring between the third and the second circles
(counting from the center).
For the area of the second circle you have .
The area of each shape is 1/5 of the total area,
since the partial areas of all shapes are equal to each other.
They want you find the width of the band for the ring between the third and the second circles
(counting from the center).
For the area of the second circle you have
 = =  ,
where ,
where  is the radius of the second circle. So, from this equation is the radius of the second circle. So, from this equation
 = =  , ,
 = =  = =  meters.
For the area of the third circle you have meters.
For the area of the third circle you have
 = =  ,
where ,
where  is the radius of the third circle. So, from this equation is the radius of the third circle. So, from this equation
 = = 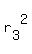 , ,
 = =  = =  meters.
Now the width of the band " a " is the difference
a = meters.
Now the width of the band " a " is the difference
a =  - -  = = 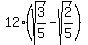 = 1.70569 meters (rounded). = 1.70569 meters (rounded).
It is your answer, and at this point the problem is solved in full, i.e. completely.
Question 1208982: Two concentric circles are drawn so that the shaded area is equal to the unshaded area. The radius of the outer circle is 8 cm. Find the difference in the radii of the two circles.
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1208635: Find the equation of a circle inscribed in a triangle with the sides on the lines x-3y=-5, 3x+y=1 and 3x-y=-11.
Found 3 solutions by math_tutor2020, ikleyn, Feliz_1965:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In the post by @Feliz_1965, this person writes
Intersection of x - 3y = -5 and 3x + y = 1: Solving this system (e.g., using elimination or substitution), we get the point (-1, 2).
Intersection of x - 3y = -5 and 3x - y = -11: Solving this system, we get the point (-4, -1).
Intersection of 3x + y = 1 and 3x - y = -11: Solving this system, we get the point (-1, 4).
No one of the given "solutions" is correct.
In other words, all three announced "solutions" are wrong.
You can easily check it by substituting the coordinates of these points,
that announced as the intersection points, into the corresponding equations.
Answer by Feliz_1965(1)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. Find the Vertices of the Triangle.
The vertices of the triangle are the points where the lines intersect. We can find these by solving the system of equations in pairs:
Intersection of x - 3y = -5 and 3x + y = 1: Solving this system (e.g., using elimination or substitution), we get the point (-1, 2).
Intersection of x - 3y = -5 and 3x - y = -11: Solving this system, we get the point (-4, -1).
Intersection of 3x + y = 1 and 3x - y = -11: Solving this system, we get the point (-1, 4).
2. Find the Angle Bisectors.
The center of the inscribed circle (the incenter) is the point where the angle bisectors of the triangle intersect. To find an angle bisector, we can use the following:
A. Find the slopes of the two lines forming the angle.
B. Find the angle between the lines using the formula: tan(θ) = |(m1 - m2) / (1 + m_1*m_2)|, where m_1 and m_2 are the slopes.
The angle bisector will divide the angle θ in half.
Use the half-angle formula to find the slope of the bisector.
Use the point-slope form to find the equation of the bisector.
You only need to find two angle bisectors, as their intersection point will be the incenter.
3. Find the Incenter.
Solve the system of equations formed by the two angle bisectors you found. The solution is the incenter (h, k) of the circle.
4. Find the Radius.
The radius of the inscribed circle is the perpendicular distance from the incenter to any of the sides of the triangle.
Choose one of the side equations.
Use the formula for the distance from a point to a line: Distance = |Ax + By + C| / √(A² + B²) where (A, B, C) are the coefficients of the line equation, and (x, y) is the incenter.
5. Write the Equation of the Circle.
The standard form of the equation of a circle is: (x - h)² + (y - k)² = r²
Substitute the incenter (h, k) and the radius r that you found into this equation.
I hope this helps.
Question 1208636: “Find the equation of a circle inscribed in a triangle with the sides on the lines x-3y=-5, 3x+y=1 and 3x-y=-11.”
Found 2 solutions by math_tutor2020, greenestamps:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The equations of the three lines, and those equations in slope-intercept form:
(1) x-3y=-5 --> y=(1/3)x+5/3
(2) 3x+y=1 --> y=-3x+1
(3) 3x-y=-11 --> y=3x+11
Solve the pairs of equations simultaneously to find the coordinates of the vertices of the triangle (I leave the details to the student)
(1) and (2): (-0.2,1.6)
(1) and (3): (-3.5,0.5)
(2) and (3): (-5/3,6)
The center of the inscribed circle is the intersection of the angle bisectors of the three angles of the triangle.
The slopes of equations (2) and (3) are -3 and 3. That means the angle bisector of that angle is a vertical line. Since the intersection of those to lines is at x=-5/3, the equation of that angle bisector is x=-5/3.
The slopes of equations (1) and (3) are 1/3 and 3. That means the angle bisector of that angle has slope 1. Knowing that those two lines intersect at (-3.5,0.5), we find the equation of that angle bisector is y=x+4 (again I leave the details to the student.)
The center of the inscribed circle is the intersection of those two angle bisectors: (-5/3,7/3). And once again I leave the details to the student.
The radius of the inscribed circle is the distance from the center of the circle to any of the three lines that form the triangle. To find that distance, use the point-to-line distance formula:
The distance from the point (p,q) to the line with equation Ax+By+C=0 is

Using (p,q) = (-5/3,7/3) and equation (2), the radius is

The square of the radius is then 121/90, so finally the equation of the inscribed circle is

You can use the graphing utility at geogebra.com to graph the equations of the three given lines and this circle to see that the solution is correct.
Question 1208632: find the equation of the circle inscribed in a triangle with the sides on the lines x-3y=-5, 3x+y=1 and 3x-y=-11
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's label the lines as  , ,  , and , and 



Furthermore, let's say the following
point A = intersection of  & & 
point B = intersection of  & & 
point C = intersection of  & & 

L1 in red, L2 in green, L3 in blue
--------------------------------------------------------------------------
The formula for the shortest distance between the point (p,q) and the line ax+by+c = 0 is:

Note: if (p,q) is on the line ax+by+c=0, then the expression ap+bq+c evaluates to 0, which leads to d = 0.
This page shows the derivation of the formula.
Here's a page showing a proof
The angle bisector is a locus of points that are equidistant from each line.
An example would be to think of the xy axis. An angle bisector of the x axis and y axis would be the line y = x. Any point on y = x is equally distant to either axis.
A point like (5,5) is 5 units away from either axis.
This equation

will allow us to find the equation of the angle bisector between the lines ax+by+c = 0 and ex+fy+g = 0. Note that the lines cannot be parallel.
A point (p,q) satisfies this equation if and only if it is equally distant between the lines. We can think of it like a midpoint.
Notice the left hand side and right hand side match the template of the point-to-line distance formula mentioned.
Rewrite x-3y=-5, 3x+y=1 as x-3y+5=0, 3x+y-1=0 so we can use them in the formula below.




 or or 
Solving  for y gets us for y gets us 
This is the bisector of angle CAB.
Part of this bisector is inside triangle ABC. If we solved the other equation for y, then we'd get an angle bisector entirely outside of triangle ABC, which means we can ignore it.
Follow similar steps to find the bisector of angle CBA is the equation 
This is a vertical line through point B.
The intersection of the angle bisectors will give us the center of the inscribed circle.
This is known as the incenter.
Solve this system  to get (x,y) = (-5/3, 7/3) which is the incenter. to get (x,y) = (-5/3, 7/3) which is the incenter.
Call this point D.
--------------------------------------------------------------------------
Once again recall that this formula

gives the distance between the line ax+by+c = 0 and the point (p,q)
We want to find the shortest distance from point D(-5/3, 7/3) to any of the three given lines. I'll use the line 3x+y-1 = 0.
Determining this distance will give us the radius of the inscribed circle (known as the inradius).




This is inradius.
So we have  which has both sides square to which has both sides square to 
--------------------------------------------------------------------------
--------------------------------------------------------------------------
Recap
We found that the incenter is at (-5/3, 7/3). These are the h,k values.
The r^2 value is 121/90
Therefore we go from  to the final answer to the final answer 
I used GeoGebra to verify the answer.
Question 1207930: The general form of an equation of a circle is given. Convert to the standard form.
2x^2 + 2y^2 + 8x + 7 = 0
Let me see.
2x^2 + 8x + 2y^2 = (-7)^2
2(x^2 + 4x) + y^2 = 49
2(x^2 + 4x + 4) + y^2 = 49
2(x + 2)(x + 2) + y^2 = 49
2(x + 2)^2 + y^2 = 49
Is this right?
Found 2 solutions by MathTherapy, math_tutor2020:
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The general form of an equation of a circle is given. Convert to the standard form.
2x^2 + 2y^2 + 8x + 7 = 0
Let me see.
2x^2 + 8x + 2y^2 = (-7)^2
2(x^2 + 4x) + y^2 = 49
2(x^2 + 4x + 4) + y^2 = 49
2(x + 2)(x + 2) + y^2 = 49
2(x + 2)^2 + y^2 = 49
Is this right?
As stated by others, your approach is WRONG.
Correct way to do this is:
Standard form of the equation of a circle:  , where: , where:  is a point on the circle's circumference is a point on the circle's circumference
 is the CENTER of the circle is the CENTER of the circle
 is the circle's RADIUS
To convert is the circle's RADIUS
To convert  to STANDARD FORM, we need to COMPLETE the "SQUARES," as follows: to STANDARD FORM, we need to COMPLETE the "SQUARES," as follows:
 ---- Placing the variables in order, and moving the CONSTANT to the right side ---- Placing the variables in order, and moving the CONSTANT to the right side
 --- Dividing EACH SIDE by 2, in order to get "+ 1" on the variables' SQUARES (x2 and y2) --- Dividing EACH SIDE by 2, in order to get "+ 1" on the variables' SQUARES (x2 and y2)

 ---- Taking ---- Taking  of b, on x, and of b, on x, and  of b, on y, and then SQUARING THEM of b, on y, and then SQUARING THEM
 ---- Adding "+ 22" and 02 to both sides of the equation ---- Adding "+ 22" and 02 to both sides of the equation

 <=== Standard form of circular-equation, 2x2 + 2y2 + 8x + 7 = 0 (general-form). <=== Standard form of circular-equation, 2x2 + 2y2 + 8x + 7 = 0 (general-form).
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I appreciate you showing your steps and thought process.
The first mistake happens when you go from
2x^2 + 2y^2 + 8x + 7 = 0
to
2x^2 + 8x + 2y^2 = (-7)^2
I'm not sure why you are squaring that -7.
Instead it should be
2x^2 + 2y^2 + 8x + 7 = 0
to
2x^2 + 2y^2 + 8x = -7
Another mistake you made is the portion going from x^2+4x to x^2+4x+4
Those two expressions are not the same thing.
What you'll need to do is add and subtract 4 to keep things balanced.
x^2+4x = x^2+4x+4-4 = (x^2+4x+4) - 4 = (x+2)^2-4
The stuff in red represents adding 0, which doesn't change the expression.
--------------------------------------------------------------------------
Here is how I would tackle this problem.
2x^2 + 2y^2 + 8x + 7 = 0
(2x^2 + 8x) + 2y^2 + 7 = 0
2(x^2 + 4x) + 2y^2 + 7 = 0
2(x^2 + 4x +0) + 2y^2 + 7 = 0
2(x^2 + 4x +4-4) + 2y^2 + 7 = 0
2( (x^2+4x+4) - 4 ) + 2y^2 + 7 = 0
2( (x+2)^2 - 4 ) + 2y^2 + 7 = 0
2(x+2)^2 - 8 + 2y^2 + 7 = 0
2(x+2)^2 + 2y^2 -1 = 0
2(x+2)^2 + 2y^2 = 1
(x+2)^2 + y^2 = 1/2 this is the equation in standard form.
The standard form template of a circle is
(x-h)^2 + (y-k)^2 = r^2
Compare that template to the stuff in red to see the center is located at (h,k) = (-2,0)
It might help to rewrite (x+2)^2 as (x-(-2))^2
It might help to rewrite y^2 as (y-0)^2
These rewrites aren't necessary if you can spot the h,k values easily at this point.
Now compare the right hand sides to find the radius.
r^2 = 1/2
r = sqrt(1/2) = 1/sqrt(2) = sqrt(2)/2
There are a few ways to represent the radius.
All of which approximate to roughly 0.70710678
I used GeoGebra to confirm the answer is correct.
Desmos is another good option.
Question 1207942: Write the standard form of the equation of the circle and the general form of the equation of the circle with radius r and center (h,k). Graph the circle.
r = 1/2; (h,k) = (0, -1/2)
Note: Circle is not centered at the origin.
Found 2 solutions by Edwin McCravy, josgarithmetic:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
And then when you get it in the standard form,
 Square the two binomials, collect terms and rearrange the terms in this
general form:
Square the two binomials, collect terms and rearrange the terms in this
general form:
 Edwin
Edwin
Answer by josgarithmetic(39625)  (Show Source): (Show Source):
Question 1207943: A. Find the center and radius of the circle.
B. Graph the circle.
C. Find the intercepts of the circle, if any.
3x^2 + 3y^2 - 12y = 0
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A. Find the center and radius of the circle.
B. Graph the circle.
C. Find the intercepts of the circle, if any.
3x^2 + 3y^2 - 12y = 0
================
x^2 + y^2 - 4y = 0
x^2 + y^2 - 4y + 4 = 4
(x-0)^2 + (y-2)^2 = 2^2
Center is (0,2)
r = 2
=====================
You can graph it on paper, or
DL the FREE graph software from several sites.
====================
x^2 + y^2 - 4y = 0
Sub zero for x to find the y-intercepts
y^2 - 4y = 0
y*(y-4) = 0
y = 0 --> (0,0)
--------
y = 4 --> (0,4)
=============
Sub zero for y to find the x-intercepts
x^2 + y^2 - 4y = 0
x^2 = 0
--> (0,0)
Question 1207939: Convert (x- 2)^2 + (y- 2)^2 = 8 to the general form of the equation of a circle.
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Convert (x- 2)^2 + (y- 2)^2 = 8 to the general form of the equation of a circle.
(x- 2)^2 + (y- 2)^2 = 8
x^2-4x+4 +y^2-4y+4 =8
x^2+y^2-4x-4y =8-8
x^2+y^2-4x-4y =0
Question 1207941: Convert x^2 + y^2 + x + y - 1/2 = 0 to the standard form of the equation of a circle.
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Convert x^2 + y^2 + x + y - 1/2 = 0 to the standard form of the equation of a circle.
x^2 + y^2 + x + y =1/2
Use completing square method for x & y
(x^2+x + (p ) )+(y^2+y+(q ) )= (1/2) + (p) +(q)
Find third term
formula =( (1/2) co efficient of middle term )^2
((1/2)*1)^2= 1/4=p = q
(x^2+x + (1/4 ) )+(y^2+y+(1/4 ) )= (1/2)+ (1/4) +(1/4)
(x+(1/2))^2+(y+(1/2)^2= 1
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085
|




