Question 971505: Can you help me multiply this quadratic equation?
121-x^2/x^2-22x+120 times x^2-24x+140/x^2-18x+77
Would I set up the 1st equation like this:
121-x^2/x^2-22x+120 =(11-x)(11-x)/(x-12)(x-10) or -(11-x)(11-x)/(x-12)(x-10)
After I did the equations but my answer differed from the answer key.
My answer was:
(x-11)(x-14)/(x-12)(x-7)
the answer key is:
(11+X)(X-14)/(X-12)(X-7)
what am I doing wrong?
Found 4 solutions by Boreal, stanbon, josgarithmetic, Theo:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! 121-x^2/x^2-22x+120 * x^2-24x+140/x^2-18x+77
Factor
[(11+x)(11-x)/(x-10) (x-12)] * { (x-14)(x-10)/(x-11)(x-7)}
The (x-10) disappears
{(x+11) (11-x) (x-12)(x-14)/(x-11)(x-12)(x-7)}
Change (11-x) to -(x-11), which is the same thing, and with a negative sign out front, you can cancel the (x-11). There does have to be a negative in the answer key.
- {(x+11)(x-14)/(x-12)(x-7)
The key is recognizing that (11-x) and (x-11) can cancel, so long as one changes the sign.
Also, 121-x^2 is a difference of squares, not (11-x)^2. It is (11+x)(11-x). The answer key still needs to have a negative.
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! Can you help me multiply this quadratic equation?
121-x^2/x^2-22x+120 times x^2-24x+140/x^2-18x+77
I would set up the 1st equation like this:
Numerator:: 121-x^2/x^2-22x+120 =(11+x)(11-x)/(x-12)(x-10)
and
Denominator:(x^2-24x+140)/(x^2-18x+77) = (x-10)(x-14)/(x-11)(x-7)
-------------
Multiply to get:
[(11+x)(11-x)/(x-12)(x-10)]
Cancel factors common to numerator and denominator to get:
[11+x))/(x-12)]
After I did the equations but my answer differed from the answer key.
My answer is:
-(x+11)(x-14)/(x-12)(x-7)
----------
Cheers,
Stan H.
-----------
Answer by josgarithmetic(39616) (Show Source):
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! see my worksheet below:
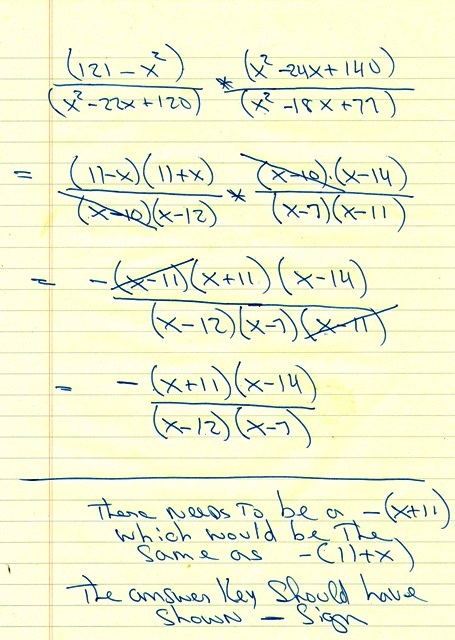
the answer key is correct except there should be a minus sign there as well which i don't see.
121 - x^2 is equal to (11-x) * (11+x)
x^2 - 18x + 77 is equal to (x-11) * (x-7)
(11-x) in the numerator is equivalent to -(x-11) which then cancels out with the (x-11) in the denominator and leaves a -1 because -(x-11) / (x-11) = -1.
|
|
|
