SOLUTION: Please help me solve this equation: {{{ (x^2-4x-8)(x^2-4x)=48 }}}

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: Please help me solve this equation: {{{ (x^2-4x-8)(x^2-4x)=48 }}}      Log On


   

Question 909147: Please help me solve this equation: +%28x%5E2-4x-8%29%28x%5E2-4x%29=48+
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Hopefully, simplification will allow an equation in quadratic form.

%28x%5E2-4x-8%29%28x%5E2-4x%29=48
x%5E4-4x%5E3-8x%5E2-4x%5E3%2B16x%5E2%2B32x-48=0
x%5E4-8x%5E3%2B8x%5E2%2B32x-48=0

Forget about quadratic form. Look for roots.
Check plus and minus of -1,2,4,6,8,24. (Rational Roots Theorem, synthetic division).

-2 is a root, giving coefficients 1,-10,28,-24.
2 is a root, giving coefficients 1,-8,12, which now represents a quadratic factor 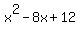x%5E2-8x%2B12.

Now you can try to factorize for x%5E2-8x%2B12=0;
%28x-2%29%28x-6%29=0
Indicating the last two roots are 2 and 6.

The original equation is equivalent to %28x-%28-2%29%29%28x-2%29%28x-2%29%28x-6%29=0
highlight%28%28x%2B2%29%28x-2%29%5E2%28x-6%29=0%29

---------------------------------------------------------------------------------------------
The solution then is highlight%28x=-2%29 OR highlight%28x=2%29 OR highlight%28x=6%29.
---------------------------------------------------------------------------------------------


The root, x=2 occurs twice, so this has a MULTIPLICITY OF 2.